For many of us fundamentals are like Swiss cheese: mostly solid but with intermittent but noticeable holes.

This is the first in a series of articles exploring the principles and properties of audio systems and related fields. Here we focus on the properties of acoustic transmission.

Perhaps you know everything on this subject already, but just maybe there are a few holes that can be filled, making the reading effort particularly worthwhile.

Q: There are two log dB scales – which one is correct to use for audio work?

Both are “Base 10” log scales, the difference being the multiplier on the front end (normally termed the “20 log10” and “10 log10” scales, and as seen in Figure 1). The log formula is a translation key, in this case a linear ratio converted to log (which is inherently a ratio).

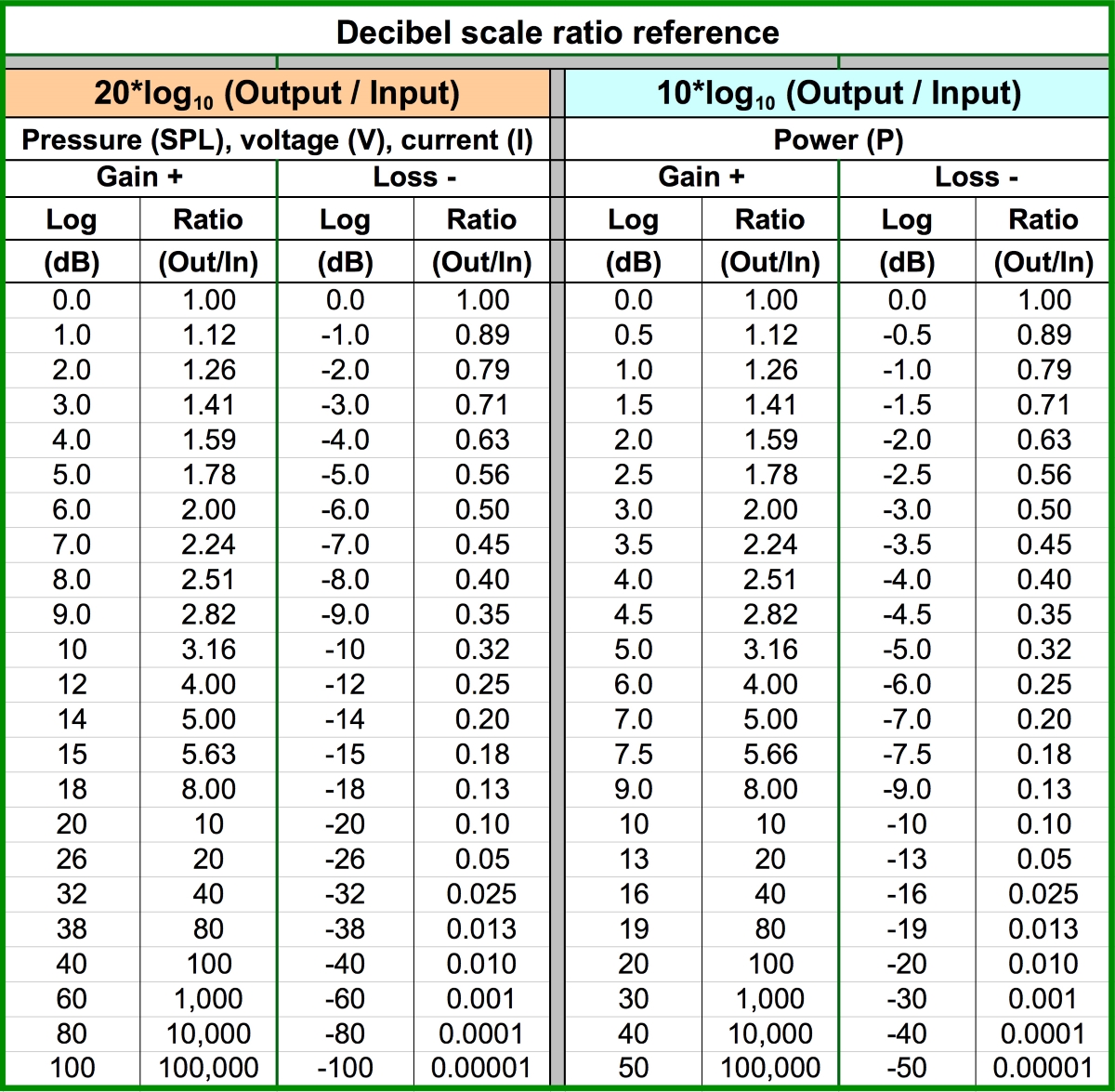
One way to memorize the 20 log10 formula is to translate it into log/linear words: a gain of 20 dB (the log side) is the result of an output/input ratio of 10x (the linear side). The 20 log scale is commonplace. It’s on every silkscreen on a mixing console – moving the fader up 20 dB increases the voltage 10x (or increased its digital numerical value by 10x). The 20 log formula applies to most of the measures we commonly express in dB: voltage (dBV or dBu), sound pressure level (dBSPL), inverse square law level loss (dB), loudspeaker array coupling (dB gain), digital audio signals (dBFS), and many more.

Meanwhile, the 10 log scale can be translated to read: a gain of 10 dB (the log side) is the result of an output/input ratio of 10x (the linear side). This is valid for power calculations (e.g., there’s a 10 dB difference between a 100-watt and 1,000-watt power amplifier).

In practice we usually use linear expressions to describe parameters that operate in the 10 log scale. For example, we rate console output in dB referenced to 1 volt (dBV), but who rates power amplifiers in dB compared to 1 watt? We see the power realm in watts (not dB), which is why the 10 dB scale is the odd bird. I can’t think of any device that has a 10 log dB scale on its user interface, but I’m open to hearing about one.

There is, however, one troublesome way the 10 log scale works itself into SPL equations and causes great confusion. The 10 log formula applies when calculating the acoustic addition of uncorrelated acoustic sources (e.g., adding the noise of a second moving light, a 2:1 linear ratio, will add 3 dB).

We use the 20 log formula when adding a second correlated source (another loudspeaker playing the same source), so in that case, the 2:1 ratio yields 6 dB of SPL gain. A lot of people get confused about this so let’s make it super clear: Metallica + Kenny G (uncorrelated) = + 3 dB; Metallica + Metallica (correlated) = + 6 dB.

Q: What is the inverse square law?

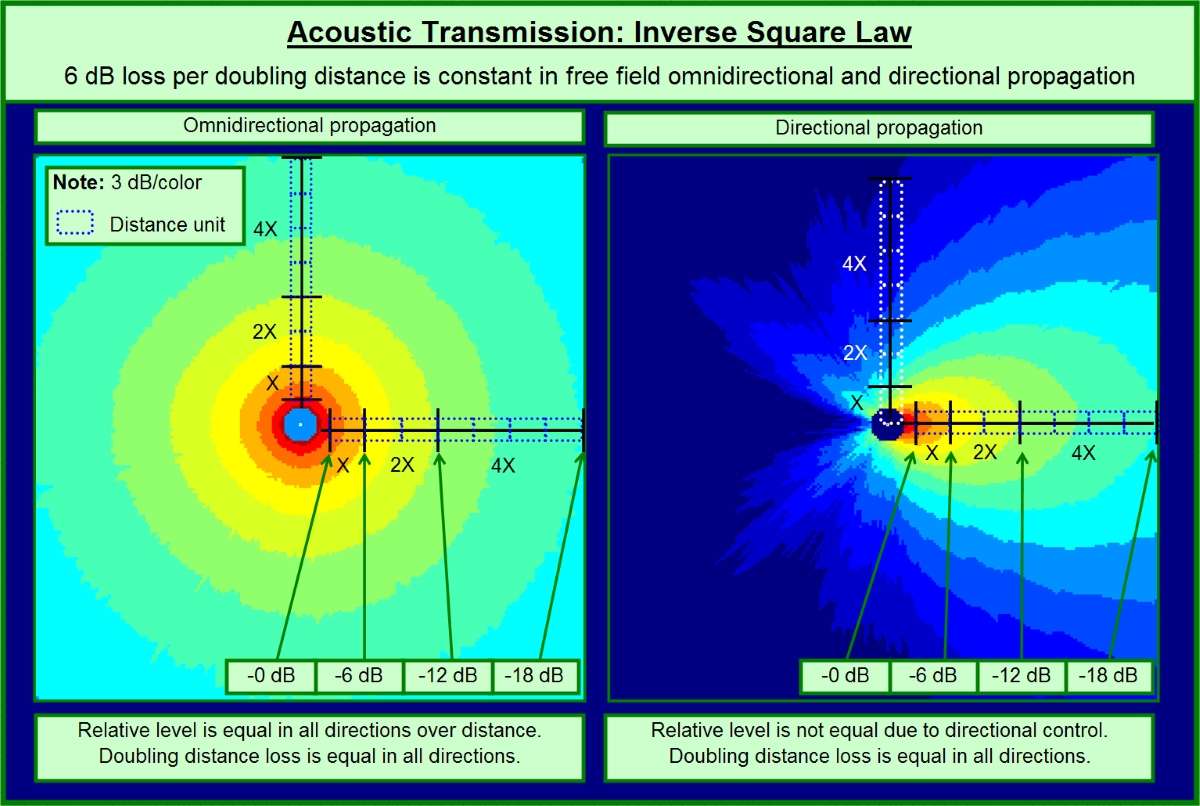
It’s the starting point for expected sound pressure level (SPL) loss over distance. Sound propagating from an infinitely small source into an infinitely large volume (no surfaces to reflect onto) will lose 6 dB per doubling of distance. For example, 106 dB SPL at 1 meter would be followed by 100 dB SPL at 2 meters.

In practice we don’t use infinitely small loudspeakers and audiences need to have a surface to sit on, so this law is not followed in absolute terms. Nonetheless it’s the best starting point. Reflections decrease the loss rate (recycled energy is added in), very high frequency air loss increases the loss rate (air is a lossy medium in the highest audible frequencies).

Is the inverse square law affected by loudspeaker directionality? Omnidirectional loudspeakers lose 6 dB/doubling distance in all directions. Directional loudspeakers start out with the on-axis side having a head start in level, but they still lose level over distance at the same rate in all directions (Figure 2).

The only way to consistently beat the inverse square law is to deploy a lot of loudspeakers and spread them out in a line. The “infinite” line source can reduce the loss rate to 3 dB/doubling as long as you have an infinite budget.