OK, I get it. This topic may be too esoteric for many, but if you’re truly interested in learning all you can about sound propagation and architectural acoustics, it’s something you should be acquainted with, at least casually.
I’m going to give you the final answer right up front. It’s either: A: 11.00”, B: 0.84”, C: 7.50”, or D: none of the above.
The question: When dealing with obstructions, which of these physical dimensions does not present meaningful acoustic shadowing in the upper speech range of audio? The answer is B: 0.84”.
But why, and how is this information unpacked and calculated?
Background
The following summarizes what I learned searching for the acoustical “k factor” equation. This journey was more complex than expected. The further I dove in, the more mistakes, misunderstandings and miscalculations I experienced. But I just couldn’t let it go. Eventually the maze began to unfold so I could grasp and understand the concepts well enough to clarify, expand on, and share with others.
If you’ve spent time working in the business of sound reinforcement it should be obvious that most sound flows or wraps around small objects and obstructions with little effort, but is blocked or increasingly “shaded” as the size of the obstruction and/or the frequencies increase.
We all recognize this phenomenon to be true. However, for the acoustician and architect, the challenge is how to better understand and calculate the range of frequencies affected by an obstruction placed between a loudspeaker and a listener, such that the obstruction may create an unwanted “acoustic shadow”?
Have you ever considered the following questions?
— How do complex sound waves navigate around various size obstructions?
— How do I figure out which frequencies will be fully or partially blocked, and which will “wrap” around objects with little loss of continuity or fidelity?
— And, how do sound waves know the dimensions of various obstructions?
The Search For “k”
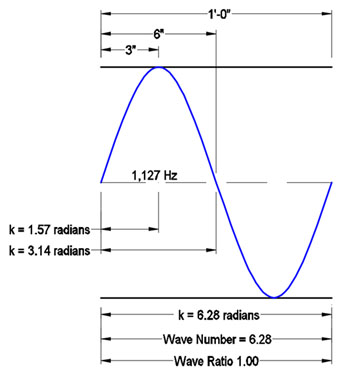
This journey started with something I remembered hearing involving the letter “k”, but I couldn’t come up with an internet search term or phrase that returned any clear answers. Eventually I discovered the “k factor” I was searching for is actually known as the “wave number,” which uses the letter k as its representative symbol.
k (always lower case) represents any wavelength that is expressed in radians. k, k number, and wave number are all synonymous and interchangeable terms.
k represents the number of full cycles that can be completed within a defined unit of distance. For acoustic applications, the wave number represents the number of radians that can be laid around the circumference of a circle that has a 1-foot radius, which is used as the baseline because the speed of sound is expressed in feet per second.