Introducing The Wave Ratio Thesis
It is proposed here that the term Wave Ratio be included in the wave number lexicon, and the acronym “kr” (all lower case) represent the unit of measurement.
kr directly represents the number of full and partial sine waves that can be completed within the linear distance of the SigDim in question.
The formula is quite simple: frequency, divided by the speed of sound, times the SigDim:
kr = f / c * a. No radians required.
For those who process this better using a specific wavelength, rather than its frequency, this is the reciprocal formula: kr = a/λ
Using kr should be easier and faster than working through k and ka calculations and conversions before any meaningful application can be considered — with one caveat: Calculating the Wave Ratio is a shorthand technique for use in architectural acoustics, where two digit resolution is adequate.
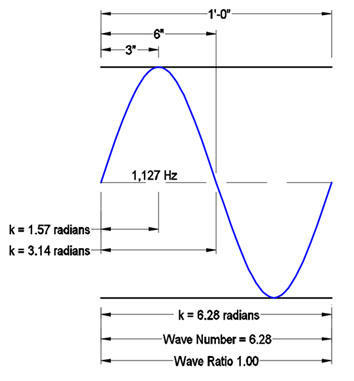
kr examples using a SigDim of 1 foot:
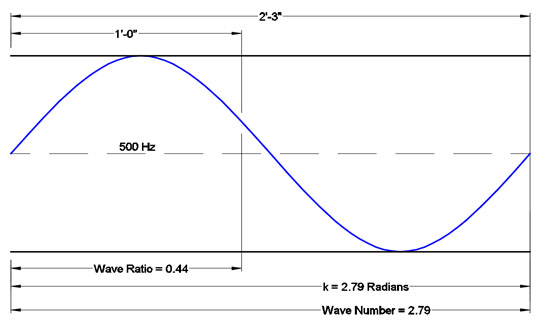
A 500 Hz sine wave has a kr of 0.44, meaning only 44% of one wave fits into 1’ (Figure 5).
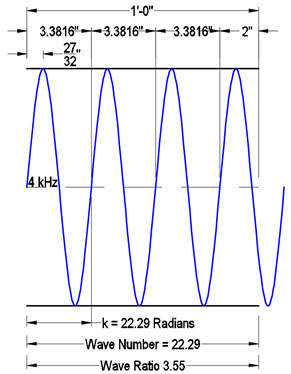
The 4 kHz kr is 3.55, meaning a 4 kHz tone can be laid across 1’, 3.55 times (Figure 6).
Extrapolating to larger or smaller SigDims is simple too. Just substitute the required SigDim in the formula, in feet. Example: If your SigDim is 15″, use 1.25’.
kr examples using a SigDim of 1.25 feet:
The 500 Hz sine wave will have a kr of 0.55, meaning 55% of one wave fits on a 1.25’ obstruction.
The 1 kHz kr is 1.11. The 2 kHz kr is 2.22. The 4 kHz kr is 4.44, meaning a 4 kHz tone can be laid across 1.25’, 4.44 times.
Why use kr?
Now that we have a mechanism for calculating the wave ratio, how does it make things simpler? And back to an earlier question, how do complex sound waves know the dimensions of an obstruction? I can tell you it’s a byproduct of kr, not amplitude. Amplitude has no bearing on this topic.
Picture this: When a complex sound wave reaches a solid boundary, certain frequencies can go no further without some blockage, or other wavefront distortion, so they don’t properly reach the listener. However, those frequencies have energy and forward momentum that has to go somewhere. Some of this energy may be absorbed, reflected, diffused, and/or diffracted, but it doesn’t reach the listener. What about the rest?
When sound waves strike a solid barrier, and are unable to proceed further, they must find an alternate path; one with less resistance. The wave energy changes direction by folding parallel to the surface of the obstruction, in all possible directions.
The folding action, which can be as much as 90 degrees in any direction, allows the momentum to be redirected so it can continue. When this happens, the various waves are redirected and spread across the SigDim. This is what makes them directly correlated. This is how the sound waves “relate” to the size of the obstruction.
Bottom line: The more times a specific frequency can be superimposed across the SigDim, the more likely that frequency will be completely blocked. Understanding this thesis leads us to a simpler way to express and calculate the relationship between a SigDim and any particular frequency or wavelength.
