Although not a new technology, manufacturers are increasingly including FIR (finite impulse response) filtering in loudspeaker processors and DSP-based amplifiers due to the significant increase in performance-versus-cost of microprocessors and DSP hardware.
The advantages of FIR filtering include more arbitrary and fine control of a filter’s magnitude and phase characteristics, independent control of magnitude and phase, and the opportunity for maximum-phase characteristics (at the expense of some bulk time delay).
The primary disadvantage is efficiency; FIR filters are generally more CPU intensive than IIR (infinite impulse response) filters. For very long FIR filters, segmented frequency-domain and multi-rate methods help to reduce the computational load, but these methods come with increased algorithmic complexity.
In pro audio, the terms FIR filter and FIR filtering are often used when referring to specific implementations, such as:
• Linear-phase crossover and linear-phase brick-wall crossover filters
• Very long minimum-phase FIR-based system EQ
• Horn correction filtering
While these implementations each have their uses, the capabilities of FIR filtering go beyond these implementations, particularly with regard to independent control of magnitude and phase as well as mixed- and maximum-phase characteristics.
So, what is FIR filtering and how does it compare to ubiquitous IIR filtering? This article aims to answer these questions but doing so first requires covering a number of basic concepts in digital audio. If you’ve studied digital signal processing, much of this will be second nature. Forgive me for skipping some of the details and simplifying some of the more complex concepts.
Key Digital Audio Concepts
Sampling. In digital audio, sound waveforms are represented by samples. An analog-to-digital converter (ADC) measures, or samples, an analog signal and assigns a digital value to each sample. Humans can typically hear frequencies between 20 Hz and 20 kHz. (A hertz – Hz – is a cycle per second.)
To adequately represent this frequency range digitally, the ADC needs to sample the audio waveform at least twice the highest audible frequency; hence we have the common sample rates of 44.1 kHz and 48 kHz. (Multiples of these frequencies, such as 88.2 kHz, 96 kHz, 192 kHz and 384 kHz are also used in pro audio, for reasons we won’t go into here.)
Half the sampling rate is called the Nyquist frequency. For example, a sampling rate of 48 kHz has a Nyquist frequency of 24 kHz.
For more information on the basics of digital audio and sampling, take a look at “Monty” Montgomery’s excellent Digital Show and Tell video and 24/192 Music Downloads article on xiph.org.
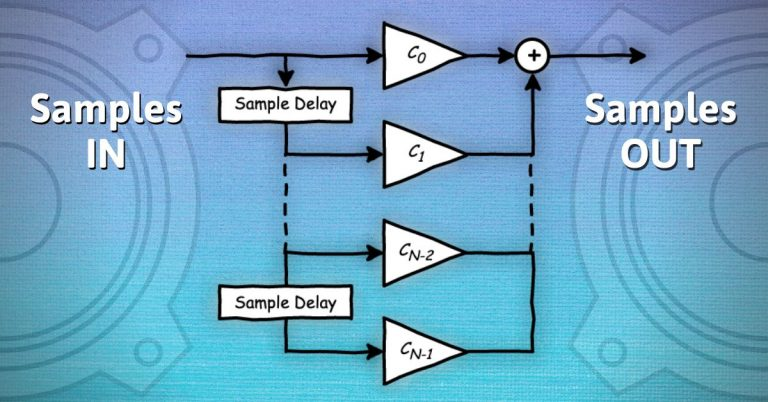
Digital Filtering. It’s a mathematical process for altering a digital audio signal. At each time interval – for a sampling rate of 48 kHz, the interval is 1/48000 seconds or 20.83 microseconds (ms) – a time-domain digital filter takes the current input sample and some previous input samples, scales (or multiplies) the samples by defined numbers, called filter coefficients, and sums the scaled samples to create an output sample.
One of the simplest digital filters is an “averaging” filter, which involves taking the average of the current and previous samples. Conceptually this is:
OutputSample = (InputSample + PreviousInputSample)/2
Figure 1 shows the filter in diagram form.
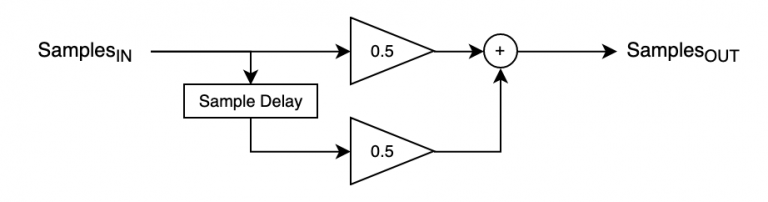
As an equation, we can express this as:
yn = 0.5 * xn + 0.5 * xn-1, where:
— xn is the input sample at the current time interval or sample number, n
— xn-1 is the input sample at the previous time interval or sample number n-1
— yn is the output sample for the current time interval, or sample number n and, the 0.5 values are the filter coefficients.
Before continuing it’s worth pausing to consider the impulse response and frequency response and how they relate to the filter structure above.