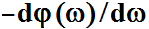In a recent discussion on my Facebook page about subwoofers, someone asked about group delay. But what is group delay? Is it the same for all frequencies like a digital delay effect? Or does it vary with frequency like phase shift? And what causes it?
I’m not a “math” guy, but all the online explanations I could find were decidedly mathematical. And even being a math whiz doesn’t guarantee a correct interpretation. In my life-long quest to understand how audio works in practical rather than theoretical terms, I’ve done many experiments. As I like to say, “Empirical evidence beats theory every time.”
I already knew that group delay causes sound from a subwoofer to emit some time after receiving the input signal – as much as a few dozen milliseconds! This delay is caused in part by phase shift inside the crossover that sends only low frequencies to the subwoofer, but a subwoofer adds its own separate delay too. So to find out how long a delay I should expect from subwoofers, my first step was to model a crossover in the freeware LTspice circuit simulation program [1].
I created a 24 dB per octave Linkwitz-Riley low-pass filter which is a standard choice for crossovers, and set the frequency to 80 Hz, standard for subwoofers in home studios (and home theaters). The filter schematic in Figure 1 is in fact a complete crossover, with both low-pass and high-pass outputs, modeled after the Rane AC-22s active crossover. Speaking of Rane, you’ll find a fabulous tutorial about crossovers, and Linkwitz-Riley in particular, at the Rane library [2].

The sine wave input source V3 at left in Figure 1 is defined as follows:
.ac = AC analysis
oct = octave (log) sweep
20 = calculate 20 data points per octave
10 = start the sweep at 10 Hz
2000 = stop at 2,000 Hz
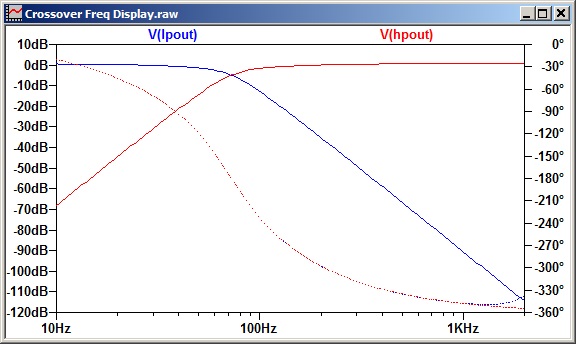
Figure 2 shows the frequency response for both the low-pass (blue) and high-pass (red) filter sections. The intersection reflects the 80 Hz/-6 dB point for both filters, with the response dB legend on the left side of the graph. The other sloping red line displays the phase shift, with its legend on the right.
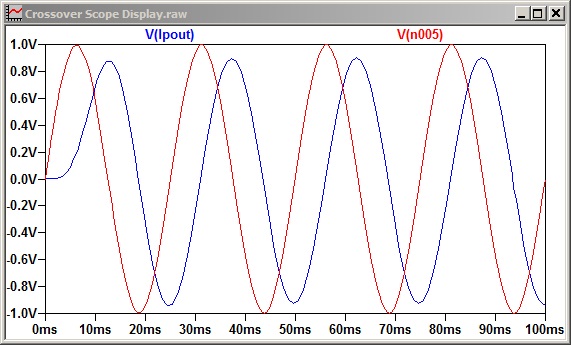
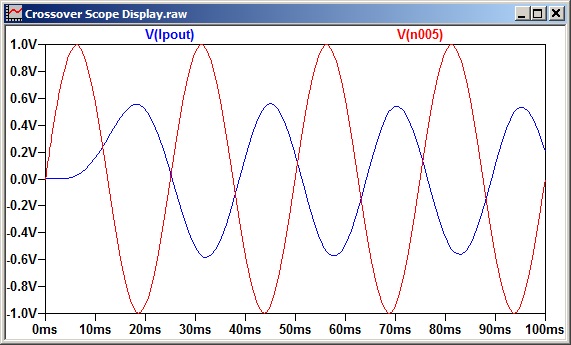
To assess the delay I measured individual frequencies from 20 Hz to 140 Hz in 20 Hz intervals, but the 40 Hz and 100 Hz frequencies in Figures 3 and 4 show all that’s needed, reporting delays around 7 milliseconds (ms) each. Of course, at 100 Hz the output is reduced because it’s above the 80 Hz crossover frequency.
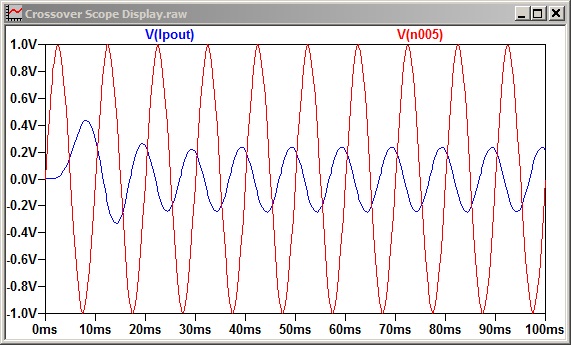
Next, Figure 5 shows the delay at 40 Hz with the crossover frequency at 40 Hz instead of 80 Hz. As you can see, the delay through the filter is now twice as long as in Figure 3. The same thing happens in the other direction and also with fewer filter poles: a 12 dB/octave low-pass filter at 80 Hz delays only half as long as 24 dB/octave at 80 Hz. But wait, there’s more…