The work of systems designers, front of house and monitor engineers, systems engineers, sales engineers, and probably several other job descriptions, can include any number of cumbersome test and measurement tools and instruments. But when all we need are quick, rough estimates, there are several easy ways to get reasonable answers with nothing but the human body and an awareness of how it’s applied.
Here, I’ll detail my on-board kit. I hope you find one or more of these tools makes your work a little quicker and easier. They have for me.
Consistent On Pitch
Ever wish you had perfect pitch? I don’t, but I do have really good relative pitch. By this I mean I can’t easily tell what note or chord is being played, but I can hear when some instrument or person is out of tune by as little as 5 cents, or 5 percent. The word “cent” stands for one hundredth of an equal-tempered semitone, and because there are 12 semitones in one musical octave, one octave consists of 1,200 cents.
Why does this matter? Where and when does good relative pitch become useful?
During rehearsal or sound check, it’s appropriate (IMHO) to help musicians and singers know when there are pitch issues that can be corrected but have yet to be recognized. Of course, you need to be consistently right. Then grace, tact and humility are required for your comments to be well received and appreciated. Believe it or not, when everyone’s pitch is locked in, your mix will sound better. (If you want to test your own ability, try the Intonation Ear Trainer game here.)
Going Low
How low can you whistle? This next one won’t be much help if you can’t whistle, but I’ll presume you can pull off a basic, lip-pucker whistle. I stumbled onto this one about 25 years ago when I got my first spectrum analyzer and have re-verified the concept with my (Rational Acoustics) Smaart rig multiple times.
The lowest tone I can whistle is an extremely consistent 500 Hz, +/- 25 Hz or so. Weird, I know, but very helpful. It’s so consistent that I’ve won a few lunch bets when I tell people I can pick, or produce, 1 kHz out of the air. I simply start with my lowest whistle tone, and then move up 1 octave. (If you struggle hearing an octave interval in your head, think about the first two notes in the chorus of the song “Somewhere Over The Rainbow.”)
This whistle trick comes in quite handy when trying to pick out feedback frequencies. I’m sure no one can whistle between 40 Hz and 16 kHz, but applying a little simple math, and an understanding of musical scales and octaves, goes a long way toward making this work.
As a sound tech, it’s really helpful if you have some basic understanding of musical notation, scales and intervals. All you really need is the knowledge and ability to whistle a major scale between the lowest frequency you can whistle, and the next one or two octaves above. In musical terms, C5 is very close to 500 Hz, so I’ll use that to help explain how to translate musical scales into sine wave frequencies.
First, find your lowest note. This may take a little practice, and a decent analyzer or phone app, so you can identify your fundamental (read lowest) whistle tone. Be sure to push out very little air to get as low as possible.
What I found really interesting is my lowest pitch didn’t change from day to day, or month to month. When I figured that out, I knew I was on to something useful. From that moment on I had a mid-band sine wave generator that’s available anywhere and anytime needed.
Plus, having good relative pitch allows me to easily whistle, or imagine – I can’t whistle much above 2 kHz, and nothing below 500 Hz, so everything else has to be imagined – the various intervals above and below my fundamental.
For quick reference, based on a tuning reference of A = 440 Hz: C0 is 16.35 Hz, and C9 is 8,372.02 Hz. C4, which is also known as middle C, is 261.63 Hz. The notes of a 1-octave, ascending C major scale are C, D, E, F, G, A, B, C. The intervals between those notes have a percentage relationship too, regardless of octave, based on their position above the fundamental C.
The major 3rd above any C is E, which is roughly 25 percent higher. The major fifth above any C is G, which is about 50 percent higher, and the A above any C is about 75 percent higher. These percentages are the key to finding other frequencies. If we translate these concepts into their corresponding frequencies, using 500 Hz for mathematical simplicity, we get these frequencies over two octaves:
C5 [fundamental] = 500 Hz (actual C5 is 523 Hz) I’ve rounded everything for simplification.
E5 [a major 3rd above 500 Hz] x 1.25 = 625 Hz (actual E5 is 659 Hz)
G5 [a major 5th above 500 Hz] x 1.50 = 750 Hz (actual G5 is 784 Hz)
A5 [a major 6th above 500 Hz] x 1.75 = 875 Hz (actual A5 is 880 Hz)
C6 [1 octave above 500 Hz] x 2 = 1,000 Hz (actual C6 is 1,047 Hz)
E6 [a major 3rd above 1,000 Hz] x 1.25 = 1,250 Hz (actual E6 is 1,319 Hz)
G6 [a major 5th above 1,000 Hz] x 1.50 = 1,500 Hz (actual G6 is 1,568 Hz)
A6 [a major 6th above 1,000 Hz] x 1.75 = 1,750 Hz (actual A6 is 1,760 Hz)
C7 [1 octave above 1,000 Hz] x 2 = 2,000 Hz (actual C7 is 2,093 Hz)
Table 1 (directly below) provides a precise translation between musical notes and their corresponding frequencies. Hopefully, you can see the repetitive patterns. I’ll leave it to you to figure out the other interval percentages if you like. Use your favorite spectrum analyzer phone app to find your lowest tone, then practice with the basic intervals outlined above.
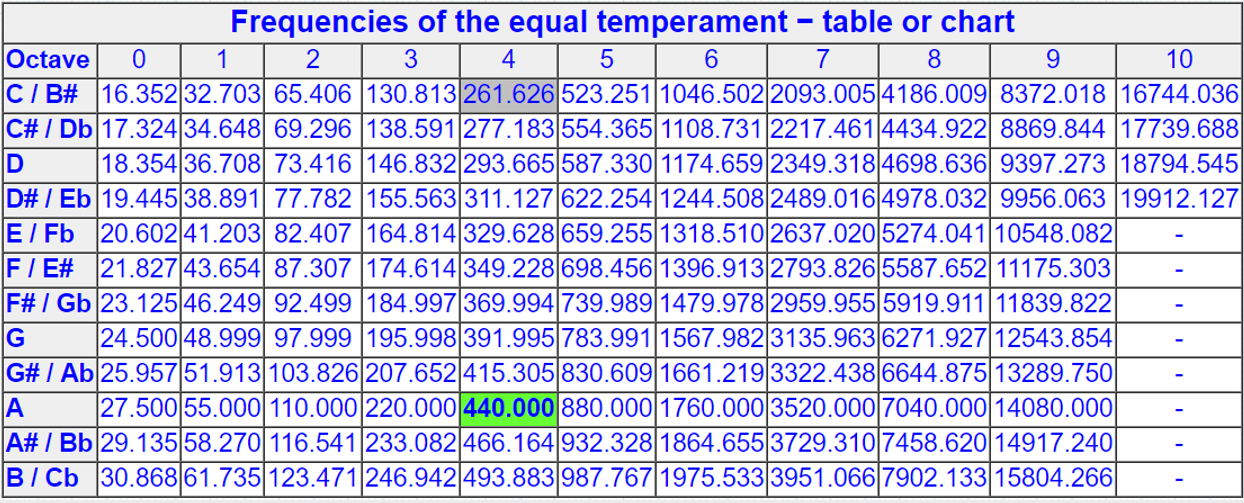
Every frequency you can hear, whistle or imaging follows these patterns. All you need to do is learn how to transpose the concept into your fundamental whistle tone. It’s the percentage above your lowest whistle frequency that’s the important point of this whole exercise. Don’t make the mistake of thinking that C5 or C6 are important or problematic frequencies; they’re not. They were picked because of my fundamental note, which was also a convenient way to explain the intervals in mathematical terms.