
Acoustic Energy Relationships. A sound wave comprises both potential energy and kinetic energy. Potential energy is energy that is stored and is ready to do work. Kinetic energy is the energy of motion.
The sum of the potential and kinetic energies is always constant, assuming a lossless transmission medium, even though each contributes a varying amount depending on the position in the oscillatory cycle.
At the extremes of the oscillatory cycle (maximum positive or maximum negative pressures) the energy is primarily potential with zero kinetic energy.
At the mid-point of the oscillatory cycle the energy is primarily kinetic with zero potential energy.
Between these limits there is a combination of potential and kinetic energies. The total energy per unit volume is called the sound energy density. Potential energy density, kinetic energy density, and sound energy density are related to each other by the equations below.
Equation 2
where,
EP = potential energy density, Joules (J)
p = acoustic pressure, Pa
κ = bulk modulus of acoustic fluid, Pa (equal to )
ρo = density of transmission medium, kg/m3
c = speed of sound, 343 ms
The potential energy is directly proportional to the square of the acoustic pressure. The bulk modulus is used to specify the volume decrease of the acoustic medium occurring under uniform pressure. Think of it as the “compressibility” of the acoustic medium.
Equation 3
where,
EK = kinetic energy density, J
ρo = density of transmission medium, kg/m3
u = particle velocity, m/s
The kinetic energy is directly proportional to the square of the particle velocity.
Equation 4
where,
E = sound energy density, J/m3
EP = potential energy density, J
EK = kinetic energy density, J
ρo = density of transmission medium, kg/m3
u = particle velocity, ms
The sound energy density in the acoustic medium is the sum of the potential and kinetic energies. Figure 4 illustrates the interaction of the potential and kinetic energies in the form of the Heyser spiral, a representation of the frequency response for a small loudspeaker separated into the real (kinetic energy) and imaginary (potential) energy relationships.
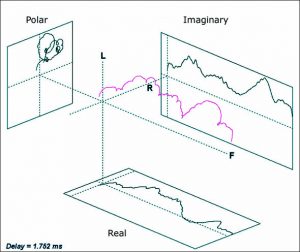
The frequency response of the loudspeaker is shown in the center between the boxes. The real (kinetic energy) response is shown at the bottom and the imaginary (potential energy) response is shown to the right. The figure to the left is the Nyquist (polar) display of both responses.
Volume Velocity. The volume velocity (U) in its most simple sense can be considered to be the amount of air that is moved by an acoustic source, such as a loudspeaker, or the amount of air that causes a transducer to move, such as a microphone diaphragm.
The units of volume velocity are m3/s. The “volume” here does not refer to level or loudness, but to occupied space as measured in cubic units.
At the boundary of the vibrating object, the acoustic particle velocity will be the same as the physical (moving) velocity of the object itself. The vibrating air particles result in an acoustic medium flow perpendicular to the vibrating object. The magnitude of the acoustic medium flow will depend on the size of the vibrating object. The volume velocity is defined by the equation below.
Equation 5
where,
U = volume velocity, m3/s
u = particle velocity, m/s
S = surface area of vibrating object, m2
The volume velocity is directly proportional to particle velocity and the surface area. Increasing either one will increase the volume velocity. The volume velocity has the same sinusoid variation and phase as the particle velocity.
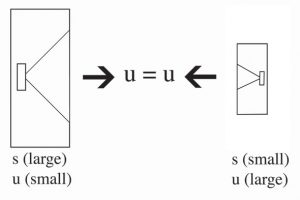
Equation 5 readily shows us that if we want to move a given amount of air, such as with a loudspeaker, we can either use a single cone (large S) with a relatively low amplitude surface (particle) velocity or use a smaller cone operating with a higher amplitude surface velocity (Figure 5).
Of importance to volume velocity is its relationship to acoustic impedance (Z). The units of acoustic impedance are Pa s/m3 and can be considered analogous to acoustic ohms. The acoustic impedance is defined by the equation below.
Equation 6
where,
Z = acoustic impedance, Pa s/m3
p = acoustic pressure, Pa
U = volume velocity, m3/s
We will see in a future article the acoustic impedance is comprised of acoustic resistance and acoustic reactance, similar to electrical impedance.
