Drop ceiling tiles are commonly found in commercial buildings, so it’s likely that in a professional audio career you will encounter them. They look decent, are cheap to install and maintain, and can cover lots of ugly utility such as wires, HVAC ducts, and sprinkler system piping.
When I get into a room to run a sound system, I like to find out as much information about that room as possible. Two basic parameters I like to discover are the Critical Frequency and the RT60, otherwise known as reverb time, a measurement of how long it would take a sound to decay 60 dB in a large room. Critical Frequency (CF) can be found using the dimensions of the room, and RT60 can be found with said dimensions and one additional step.
A brief description of the CF is the approximate frequency where the room’s natural modes (standing waves) dissolve into a diffuse sound field. Below this frequency room modes dominate and really the only way to fight it besides bass traps is to not excite the modes in the first place. In corporate sound this often means a high-pass filter set around the CF.
The CF is calculated by taking the Mean Free Path, which is the average distance between the walls, floor and ceiling. As the wavelength of the sound approaches this distance, modal tendencies ensue. The larger the room dimensions, the longer the mean free path and conversely, the lower the frequency of the CF. Most good-sized ballrooms have a CF around 125 HZ.
The next consideration is the reverb time of the room. This describes the time it takes for sound to decay 60 dB or 1,000,000th of the power level of the initial sound. This is a fairly complicated equation in which the answer is derived from room dimensions and what’s known as the absorption coefficient, a term coined by Wallace Sabine around the turn of the 20th century.
The important part to know about the Sabine equation for reverb time, or the Norris-Eyring equation that I use, is that it is only describing the reverb time for one particular frequency. You have to re-enter info for a different frequency and solve again if you desire. This becomes important as we will see coming up.
What this is all leading to is the question: should a drop ceiling be considered the ceiling of a room? Different “Height” measurements for a room will shift the CF and the RT60. I took the liberty of taking several measurements in my home studio since it has a drop ceiling.
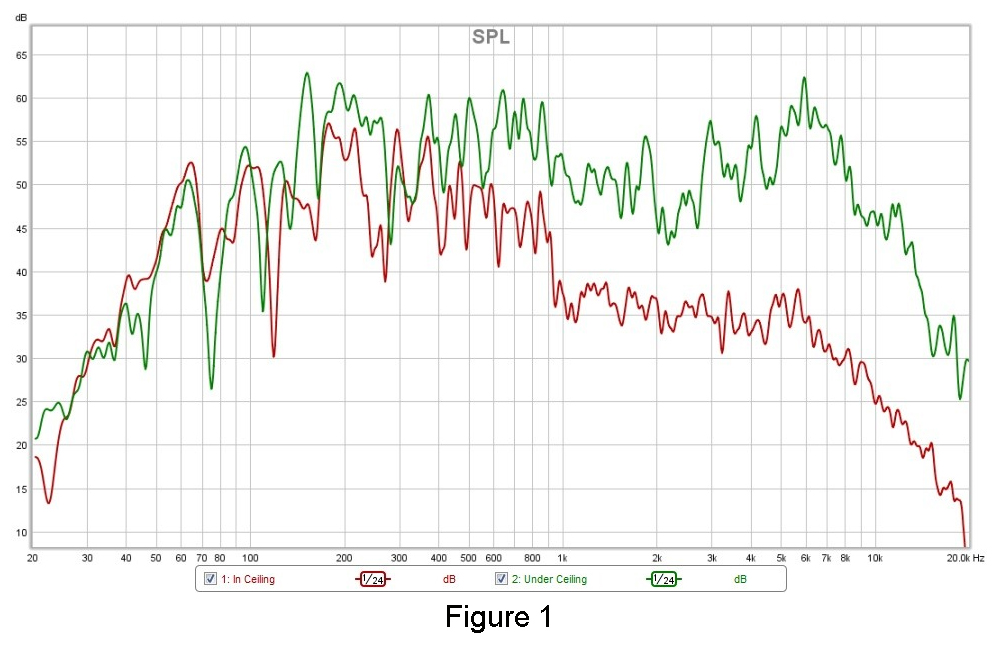
The tiles are 1/2-inch or 1.27 centimeters thick. Figure 1 presents an FFT (fast Fourier transform) measurement of a microphone placed up behind the drop ceiling (red) and just under the tile in the room (green). Both were about 6 feet (1.82 meters) from the loudspeaker and were very off-axis. The loudspeaker sat perpendicular to the ceiling on a stand.
Room modes can occur up to about 500 Hz in small rooms, and the CF is usually between 40-200 Hz for a ballroom or sanctuary. As you can see, in the low frequencies the ceiling tile didn’t really do much to the response. Those long wavelengths pass right through it at nearly the same level.
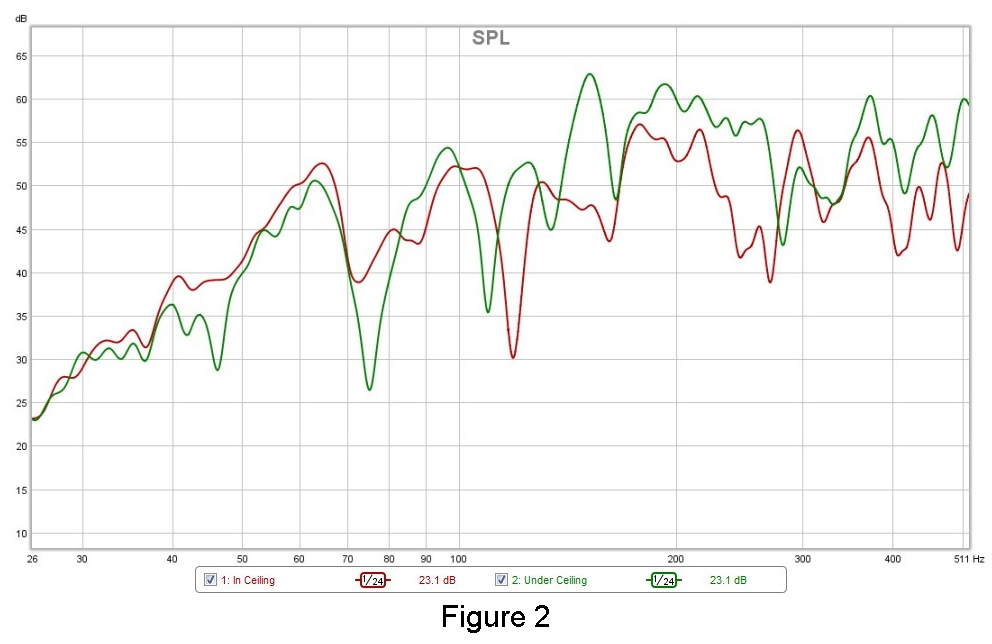
When calculating the CF, we also need to consider the higher timber or floor boards of the structural ceiling. Figure 2 shows is the lower region zoomed in.
Now if I was considering the RT60 of say, 8 kHz, because it loses 20 dB from going through the tile, I see it best to consider the tile as the ceiling height. Most of the 8 kHz energy will be absorbed or reflected off of the tile.
To make life easier for myself I made an Excel calculator that does all of the Critical Frequency and RT60 math for me. The only needed input is the dimensions of the room and the average absorption coefficient of the surfaces. It is available here, free of charge. Start with “Read Me.”