Welcome to the third part of a series of articles exploring the principles and properties of audio systems and related fields (Part 1 is here and part 2 is here).
This time we focus on the properties of audio summation. Perhaps you know everything on this subject already, but just maybe there are a few holes that can be filled in and make the reading effort worthwhile.
Combine two equal level sources: Do we get +3 dB or +6 dB?
The correct answer is yes. And there are even more possible outcomes as well. There’s a lot of confusion on this subject in the pro audio community so let’s set the record straight.
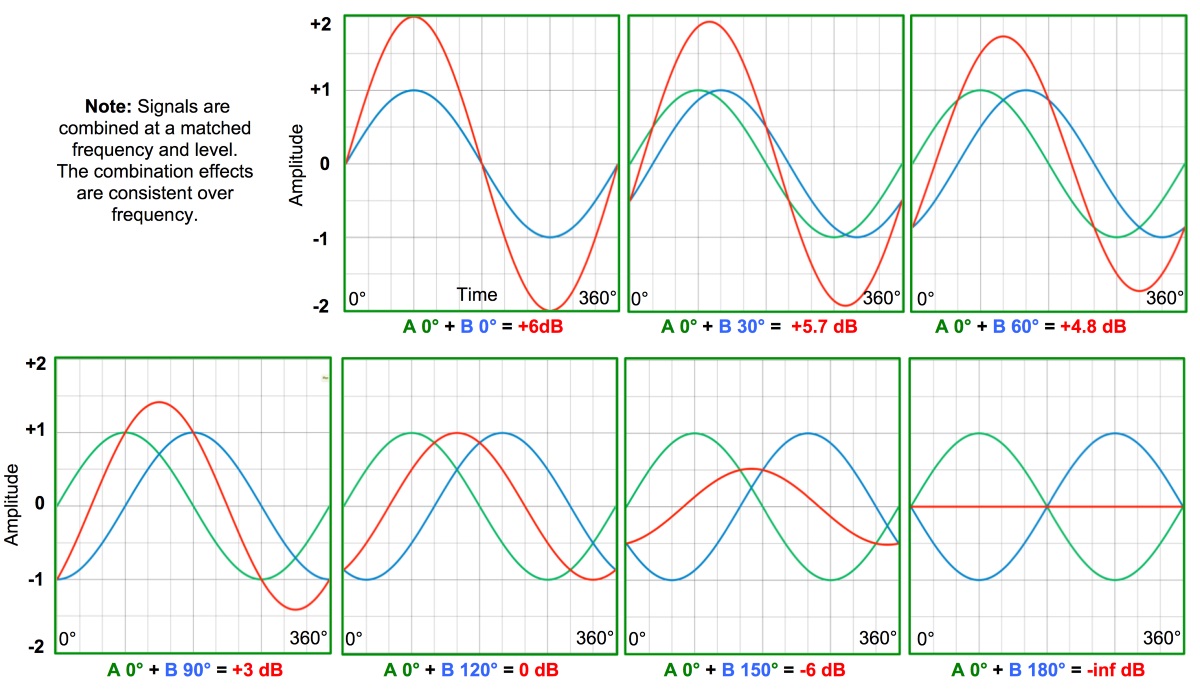
Summation results depend on two critical ingredients: relative amplitude and relative phase. If the two signals are matched in level and phase then we get a doubling (2x, i.e., + 6 dB). This seems pretty straightforward, and yet there are readers out there that are thinking “I heard it was +3 dB.” So if these are both right, then what is the differentiator?
Correlation. In order for the summation result to be consistent over time (which we call a “steady state” value), the signals must be correlated. They must be the same song with a constant relative amplitude and phase relationship. This could be steady state addition (up to +6 dB) or cancellation (down to – 60 dB or so).
The maximum addition (matched level and phase) is simply the same song at twice the size. Let’s call it 1 + 1 = 2. The maximum cancellation (matched level and inverted phase) is one copy of the song subtracted from the other. Let’s call it 1 – 1 = 0. Intermediate relative level and phase values will provide combinations between these extremes but (importantly) they will be steady and predictable (Figure 1).
If the signals are uncorrelated, such as Metallica and the Metropolitan Opera, then the relationship between the signals changes over time. On a moment-to-moment basis the signals can have any combination of level and phase relationships, and the combined result is a new and unique musical composition: Metallicopera. The combined result can still run the complete range of outcomes (between +6 dB and -60 dB) but the outcome is neither constant nor predictable. The relative level and phase values are random.
There are two certainties in this situation. The first is the uncertainty of the combined level at a given moment. The second is that two signals mixing together is more than one of the signals alone (duh!). That is where the +3 dB figure comes from: sources that get added together as strangers, rather that twins. The + 3dB figure is not exact for any given moment but is the combined statistical average over time of uncorrelated sources with matched average levels and random phase.
Here’s an example to help clarify the difference in the +3 dB (uncorrelated) and +6 dB (correlated) scenarios: A restaurant with everyone talking separately (uncorrelated) compared to when everyone sings “Happy Birthday” in unison (correlated). Send pink noise and add a matched loudspeaker (+6 dB). Listen to the noise floor and add a second moving light (+3 dB).
What happens when we sum multiple (more than two) signals?
We’ve memorized that each time we double the number of loudspeakers we gain 6 dB (2x = +6 dB, 4x = +12 dB, and so on). But what about 3x and 5x and other quantities that are not simple doublings? What is the difference between 8 boxes and 10 boxes?
The problem here is that many of us have memorized the doubling answers without internalizing the mechanism behind them. The key to understanding this is the knowledge that these dB values are the log coded version of the linear ratio relationships. For example, +12 dB is the log version of a 4:1 ratio. So if we go from 1 loudspeaker to 4 we get +12 dB. We could read the log version of this as 0 dB + 0 dB + 0 dB + 0 dB = 12 dB. That makes no sense in its log coded form, since adding an infinite number of zeros doesn’t normally make something larger or louder. The reality is that 0 dB is not “zero” in the linear sense. It’s a ratio of unity, i.e., 1:1. Translated to linear ratios the previous equation reads: 1 + 1 + 1 + 1 = 4. Not so complicated, eh?