Making It “F”
Viewing the DFT in this way, it’s easy to see where the algorithm can be optimized.
First, note that all of the sine probes are zero at the start and in the middle of the record—no need to perform operations for those.
Further, all the even-numbered sine probes cross zero at one-fourth increments through the record, every fourth probe at one-eighth, and so on. Note the powers of two in this pattern. The FFT works by requiring a power of two length for the transform, and splitting the the process into cascading groups of two (that’s why it’s sometimes called a radix-2 FFT).
Similarly, there are patterns for when the sine and cosine are at 1.0, and multiplication is not needed. By exploiting these redundancies, the savings of the FFT over the DFT are huge. While the DFT needs N^2 basic operations, the FFT needs only NLog2(N). For a 1024 point FFT, that’s 10,240 operations, compared to 1,048,576 for the DFT.
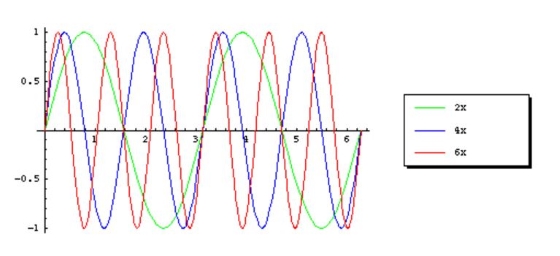
Let’s take a look at the kinds of symmetry exploited by the FFT. Here’s an example showing even harmonics crossing at zero for integer multiples of pi/2 on the horizontal axis:
Here we see that every fourth harmonic meets at 0, 1, 0, and -1, at integer multiples of pi/2:
Caveats And Extensions
The Fourier transform works correctly only within the rules laid out—transforming a single cycle of the target periodic waveform. In practical use, we often sample an arbitrary waveform, which may or may not be periodic. Even if the sampled waveform is exactly periodic, we might not know what that period is, and if we did it may not exactly fit our transform length (we may be using a power-of-two length for the FFT).
We can still get results with the transform, but there is some “spectral leakage.” There are ways to reduce such errors, such as windowing to reduce the discontinuities at the ends of the group of sample points (where we snipped the chunk to examine from the sampled data). And for arbitrarily long signals (analyzing a constant stream of incoming sound, for instance), we can perform FFTs repeatedly—much in the way a movie is made up of a constant stream of still pictures—and overlap them to smooth out errors.
There is a wealth of information on the web. Search for terms used here, such as Fourier, FFT, DFT, magnitude, phase… The purpose here is to present the transform in an intuitive way. With an understanding that there is no black magic involved, perhaps the interested reader is encouraged to dig deeper without fear when it’s presented in a more rigorous and mathematical manner. Or maybe having a basic idea of how it works is good enough to feel more comfortable with using the FFT. You can find efficient implementations of the FFT for many processors, and links to additional information, at www.fftw.org. For another source on the transform and basic C code, try Numerical Recipes in C.
Read and comment on the original article here.
Nigel Redmon is a musician, electrical and software engineer, and independent developer, specializing in digital audio signal processing applications. He has developed products for Line 6, Equator Audio, Alesis, Oberheim, and others.