The setting of delay times in signal processors is one of the principal techniques of system optimization. In most cases the timing is set to “align” two (or more) signal sources so as to create the most transparent transition between them. The process of selecting that time value can be driven by time or phase, hence the relevant terms are “time alignment” and “phase alignment.”
These are related but different concepts and have specific applications. It’s important to know which form to use to get your answers for a given application.
Time alignment connotes a synchronicity of sources, e.g., they both arrive at 14 milliseconds (ms). Phase alignment connotes an agreement on the position in the phase cycle, e.g., they each arrive with a phase vector value of 90 degrees.
Time alignment is most applicable when the sources are matched and have the same operating frequency range, e.g., a full-range main loudspeaker and the same model used as a side fill. Phase alignment is called upon when sources cover different frequency ranges, e.g., mains and subs.
Both time and phase alignment together may be required when unmatched sources cover matched frequency ranges, e.g., Papa Bear mains, Mama Bear side fills and Baby Bear delays. These are the broad strokes. Now let’s dig deeper.
And They’re Off…
How can we explore a complex subject such as phase and time without resorting to “click-to-the-next-article math”? We will use both analogy and pictures of the real stuff in action.
The first analogy is a relay race. The first runners are aligned to a single starting point. The race begins with the starter pistol, the moment of time alignment between all sources. If the runners travel at the same speed, they are both phase aligned (their radial position on the track) and time aligned (the elapsed time puts them the same distance from the start). If one runner goes faster than another, then both phase and time fall out of alignment. If the difference reaches a complete lap, then the phase is aligned (again) but the time is not.
It’s a relay race, which means the first runner for each team must hand off the baton to the second. The critical element here is that the two runners on our team must be phase aligned to make the handoff. The second runner intersects the first at the designated radial meeting point (the phase) regardless of the time (one team may be ahead of another but the handoff occurs at the same place). Each handoff is a “crossover” of the baton to another member of the team.
Our 3-way sound system is like a relay race, with tweeter, midrange and subwoofer running the segments. They must be phase aligned at each crossover to keep from dropping the sound to the ground and blowing the race.
Terminology
Let’s go through a bit of phase terminology to standardize the discussion, specifically: phase shift, phase delay, phase offset and phase alignment. Phase shift is frequency-dependent delay quantified in degrees, phase delay is the same thing quantified in ms, and phase alignment is the process of phase matching at a particular frequency and location.
The term “group delay” is used by some for phase delay but the distinction is not relevant here. Let’s illustrate by example: A filter attenuates the amplitude and causes the phase response to bend 90 degrees at 1 kHz: phase shift of 90 degrees or phase delay of 0.25 ms. The same would go for a loudspeaker that has low frequencies lagging behind the highs (as in 99.9 percent of loudspeakers). One loudspeaker has 90 degrees of phase shift at 1 kHz and the other does not: phase offset of 90 degrees or 1/4 wavelength (the difference).
Time offset terminology is easier because it is frequency independent. Time offset causes phase offset, however, which is frequency dependent. A time offset of 1 ms causes 3,600 degrees of phase offset at 10 kHz, 360 degrees at 1 kHz, and 36 degrees at 100 Hz.
Applications
The easiest way to visualize the need for time alignment is mismatched latency between devices in a common path. Latency is frequency independent, so the difference is a fixed time offset. The solution is time alignment by delaying the earlier signal.
The propagation time of a sound source through air is effectively “acoustic latency.” Two matched loudspeakers arriving from different acoustical path lengths have a latency offset that can be compensated by time alignment.
Phase alignment comes into play when devices have unmatched phase responses over frequency. This should be a minor issue in analog electrical signals unless they’re unmatched in terms of their upper and lower limits.
Differences in AC coupling filters at the bottom end and TIM filters at the top end can cause phase offsets around the extremes. One solution could be exotic phase alignment filters, but the simplest would be matching the amplitude responses first, which may reduce or eliminate the phase differences.
Time alignment is straightforward. We can use the impulse response of a modern analyzer and read the time offset directly. This is true any time the ranges of the devices being aligned are matched over the large majority of their ranges. They don’t have to be exact.
For example, a typical underbalcony loudspeaker has more very high frequency response and less low frequency range than the mains, yet time alignment should work fine because they have 6-plus octaves of overlap. Subwoofers ranging from 30 Hz up to 100 Hz can be merged with mains covering down to 60 Hz. There’s less than an octave of overlap, which means time alignment is a poor choice (phase alignment is used).
Moving Targets
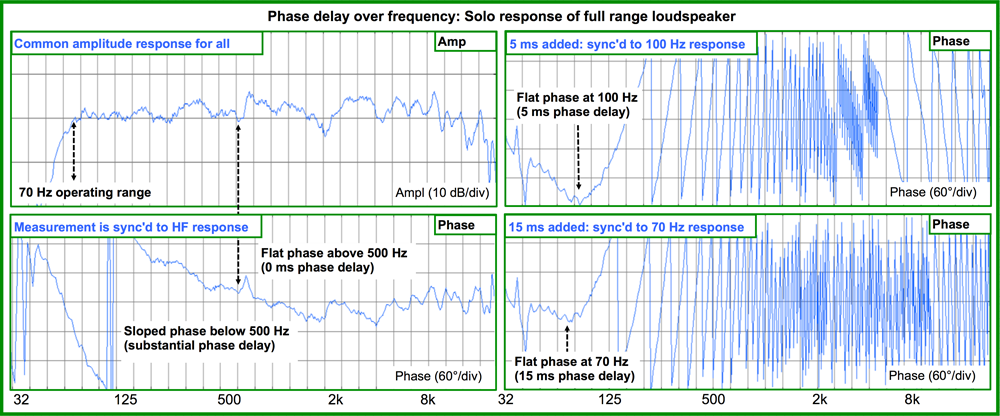
Now let’s get to the tough reality about loudspeakers. They have lots of phase shift and phase delay. A good quality active loudspeaker can be engineered to keep the range from 500 Hz on up within ±60 degrees of phase shift (less than 1 ms of phase delay). By 100 Hz we can expect 5 ms of phase delay, rising rapidly below that.
This is important because in the LF range, the loudspeaker can’t be characterized as having a single arrival time. It has arrival times that span a very large range. For example, a 2-way system that reaches down to 70 Hz might have 10 to 15 ms of phase delay at the bottom (Figure 1).
A subwoofer covering from 30 Hz to 100 Hz typically shows more than 30 ms of phase delay between its upper and lower range, with a continuous range of values in between (Figure 2). We kid ourselves when we say the sub energy arrived at the mix position at 100 ms because it actually arrives spread over a 30 ms range around that.
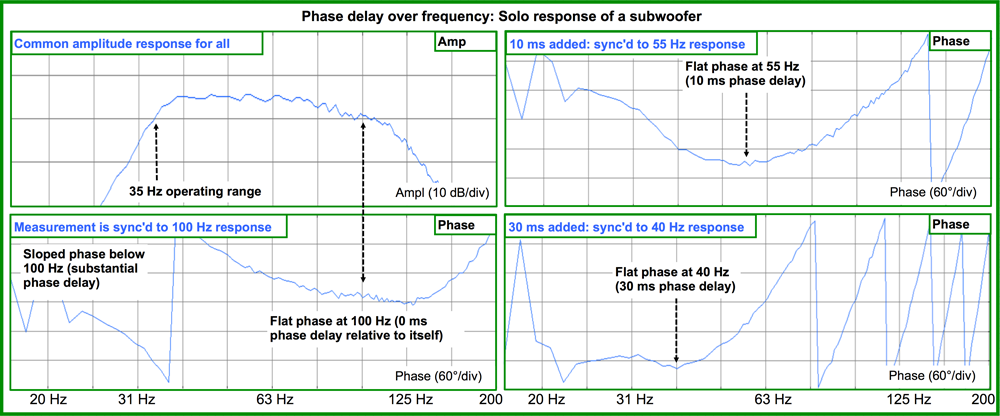
The mains, by contrast, have widespread agreement about arrival time, with their upper six octaves all within 0.5 ms (at least the good ones do). This is why you see that beautiful impulse spike.How can we time align a thing that has 30 ms of slop factor over a course of two octaves? If you ever wonder why your analyzer has a hard time finding an impulse on subwoofers, think about the fact that the energy is spread over time – a lot of time. The ambiguous impulse response reading of the analyzer is the result of the temporal ambiguity of the system being measured, not the analysis method (even if you stretch out the measurement window and restrict the measured bandwidth).
The causes of LF phase delay accumulation are a complex mix of electroacoustic behaviors and filters (maybe another article, another day), but the trend is observable on virtually any loudspeaker. Therefore our main array has phase shift (phase delay) that increases in the low end.
Matched models have matched phase delay, which means they have no phase offset (and hence no time offset). Such a matched pairing is inherently phase compatible. Any phase offset between them would have to be the result of time offset (such as a longer path) and would be remedied (if desired) by time alignment (Figure 3).
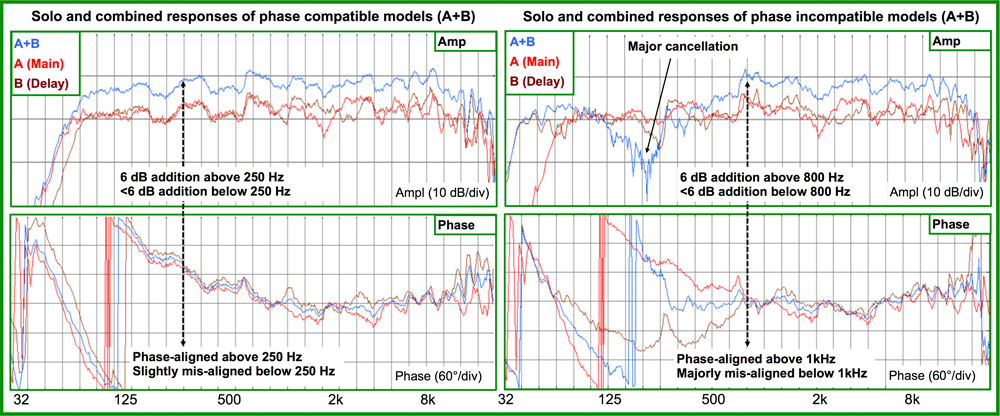
A marriage between 2-way and 3-way systems is a classic phase compatibility challenge. All-pass filters are the most typical tools for phase alignment of incompatible models.A different loudspeaker model may accumulate phase shift at a different rate over frequency, and therefore we will find phase offset begin to accrue between the pair.
This is like the relay race where one team is faster than the other. If the amount of phase offset is small, we would classify the pairing as “phase compatible,” which means time alignment is still an applicable tool. If the offsets are large, then we will need to use both time alignment (to synchronize the compatible areas) and phase alignment (to reduce phase offset in the incompatible areas).
Making Connections
Now on to our second analogy: freight trains. When did the train cross Main Street? The first car crossed at 12:00 but the last one did not cross until 12:05. Our loudspeakers cross the mix position like that.
First the highs, and then later, the lows. Let’s give each octave it’s own car and see how it works (Figure 4). If we had a loudspeaker with 4 ms of phase delay per octave, we would see evenly sized cars that are a total of 36 ms long.
Now let’s move this closer to audio reality. The first six cars (16 kHz to 500 Hz) are so small they only occupy 0.5 ms of track, but after that the cars get bigger and bigger until they stretch all the way to 36 ms (like the previous one).That would be a terrible loudspeaker, but stick with me here. We could have another train running next to it on a parallel track. Each car would line up to its counterpart, i.e., the trains have lots of phase delay but zero phase offset. They are time aligned.

If we run this train next to the first one, they will match at the first and last cars – but the middle cars don’t match. The front and rear cars are time aligned but the middle section is full of phase offset. The systems are not “phase compatible.”
How do we connect a main train to a subwoofer train? This is a series connection (unlike the time alignment on the parallel track). Connect the rear of the main train to the front of the subwoofer train. The cars are phase aligned at the coupler between the two sections.
The Process
We can time align a full-range loudspeaker to a full-range loudspeaker or a subwoofer to a subwoofer since each pairing covers the same range. It’s when we want to marry mains to subs that time alignment goes out the window in favor of phase alignment.
The same principal applies for a crossover between an HF driver and a LF driver in a 2-way box, but in the modern world, this is handled by the manufacturers, right?
So how do you do it? That’s the easy part. Time alignment is a 3-step process. Use the impulse response because it will give readings directly in the applicable unit: time. Observe the impulse response of A (solo), and then B (solo), and delay whoever got there first.
Then take a look at the frequency responses and verify that maximum addition has occurred. A little trick here is to observe the highest frequency range bump the delay up or down by the smallest allowable increment (e.g., 0.01 ms) and see what gives the best addition.
Phase alignment follows the same steps, but we are going to use the phase response instead of the impulse. Look at A solo, then B solo, and add delay to the early one until the phase responses match (Figure 5). Polarity inversion can be considered in cases where this allows for a smaller amount of delay to be used.
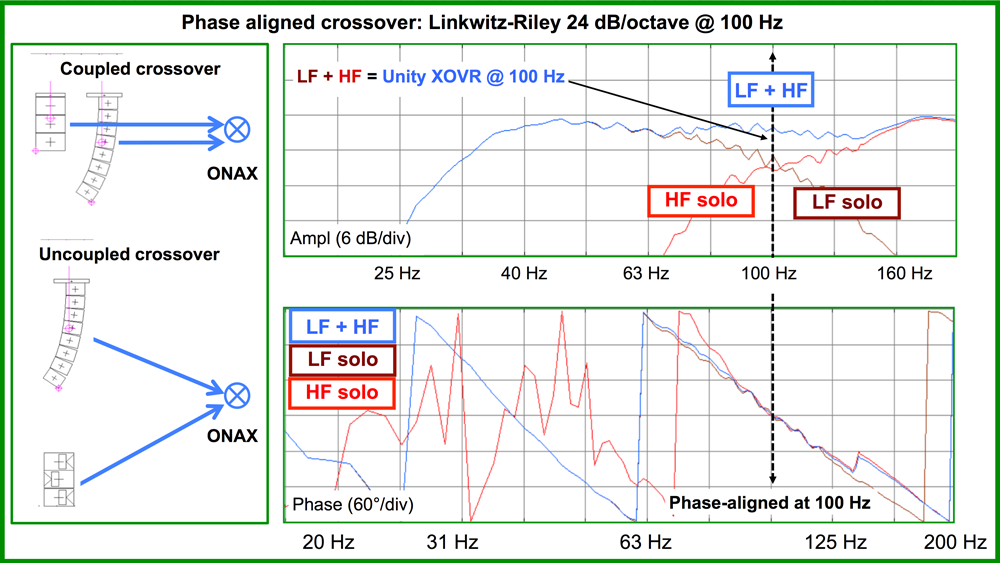
There are many ways to approach the alignment of sources that mix together. All of them affect phase and time. It’s very helpful to know which of the alignment paths is most suitable to your particular application.For example, a 100 Hz crossover might be phase aligned by 7 ms of delay on the subs or 2 ms and a polarity reversal. The later approach minimizes the overall time spread over the spectrum. Another approach to minimize overall time stretching could be all-pass filters in the affected area.
Bob offers special thanks to Merlijn Van Veen for his help with this article.