Line arrays get the lion’s share of attention these days – and that’s no surprise because they’re big and loud, and dare I say it, glamorous.

But the truck rarely rolls without a complement of two-way loudspeakers sporting a 12-inch or 15-inch woofer and a horn. Whether its monitor wedges, drum fill, front fill or just “speakers on sticks,” small 2-way boxes do many of the everyday jobs that make up a typical sound reinforcement day.

We take the performance of these boxes for granted, but they can be used to better effect if we really understand their directivity characteristics and what makes them perform the way they do. They’re often described as a 90 by 60 box or some other dubious reference.

But 90 degrees by 60 degrees at what frequency? Certainly not from DC to light.

There are four principal ingredients that govern the dispersion pattern of these loudspeakers, including the cone driver, horn, crossover and cabinet. Let’s look at these one at a time and assess their contributions.

Before we go through our list, though, let’s review some basics. The amount of directivity any device can exert on a sound wave is directly related to the proportional sizes of the device and the sound wave.

To understand this relationship it is important to have a good grasp of how wavelength relates frequency. Sound at sea level at 72 degrees Fahrenheit travels at approximately 1,130 feet per second. We express frequency or cycles (sine waves) per second as Hertz.

So if the frequency of a wave is 1Hz, the wave is 1,130 feet long. Logically, a 10 Hz wave is 113 feet long, a 100 Hz wave is 11.3 feet long, and a 1000 Hz wave is 1.13 feet long, etc. While it’s not overly difficult to do the math to determine the wavelength of any given frequency, there is an old “cheat” called the rule of 5-2-1:

20 Hz = 50 feet
50 Hz = 20 feet
100 Hz = 10 feet
200 Hz = 5 feet
500 Hz = 2 feet
1,000 Hz = 1 foot
2,000 Hz = .5 foot
5,000 Hz = .2 foot
10,000 Hz = .1 foot

While not perfectly accurate, it fills the bill for “quick and dirty” calculations. Physics dictates that a source be physically large in comparison to a wavelength to exert directional control over it. With all of this in mind, let’s look at the low frequency directivity of a 12-inch driver in a 2-way loudspeaker with a 90-degree by 60-degree horn.

Matter Of Control

Remember that the low frequency driver’s only means of controlling the dispersion of the sound wave in a front-loaded loudspeaker are its cone diameter, and to a lesser extent, some boundary effects (we’ll discuss that later). At 100 Hz, the driver is physically small in comparison to the 10-foot wavelength and provides almost no directivity (Figure 1).

If we increase the frequency gradually, the 12-inch driver does not suddenly exert pattern control over the sound wave when it reaches 1,000Hz (1 foot), and is the same size as the driver itself. Rather, it has more and more effect as the frequency gets higher and the wavelengths get shorter. (Figure 2 & Figure 3).

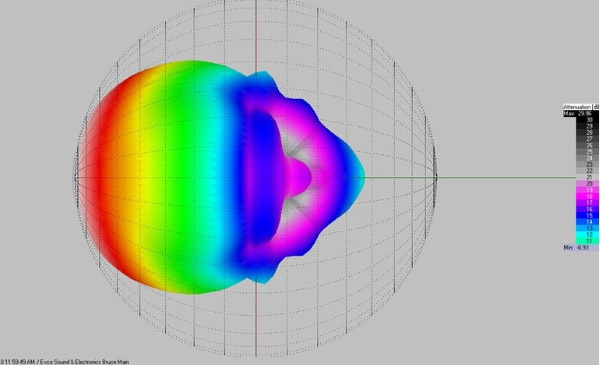
In this frequency range, the cone driver is actually providing approximately 90-degree horizontal dispersion. But also realize that since this pattern is conical (the driver is round), it is not producing the specified 60-degree vertical pattern.

As the frequency increases the driver exerts more and more control until it begins to “beam” at higher frequencies. But by the time it narrows that much, it’s above the crossover frequency.

This particular loudspeaker crosses over about a half-octave above the balloon in Figure 3. This has an overriding effect on the polar behavior of the box, especially in the vertical domain, so we will discuss the range from 1,000 Hz to 1,500 Hz when we discuss the crossover.

Now, on to the horn.

Desired Directivity

There are multiple elements in a horn’s design that contribute to its ability to achieve pattern control at a given frequency. Some of them are throat geometry, length and flare rate.

But the most obvious factor is the size of the horn mouth. The same rules apply here as to the cone driver. Size matters. The horn mouth must be large enough to dominate the wavelength in question in order to provide complete directivity at that frequency.

So, if a horn mouth is 6 inches wide by 3 inches tall it will be somewhat omnidirectional at 1,000 Hz. It will not exhibit the desired directivity until the frequency reaches about 2,000 Hz in the horizontal plane and 3,000 Hz in the vertical plane. It may provide a 90-degree by 60-degree pattern above 3,000 Hz, but almost certainly not at lower frequencies.

Cone drivers and horns by themselves are fairly predictable devices. But combining the two in close physical proximity can be quite challenging.

The first problem is physical offset. In a typical 2-way box, the devices are located one above the other and may also be at different depths. Even if we use delay to correct the time alignment between the drivers on axis, any other vertical angle will skew the time arrivals from the horn and the cone driver.

Because the bandpasses and vertical dispersion patterns of the drivers necessarily overlap in the crossover region it is probable that at any vertical angle that is off axis we will be hearing contributions from both drivers out of phase. This means there will be lobes and nulls. (Figure 4 & Figure 5) This particular box was crossed over at 1,350 Hz with a symmetrical Linkwitz-Riley 24 dB slope.

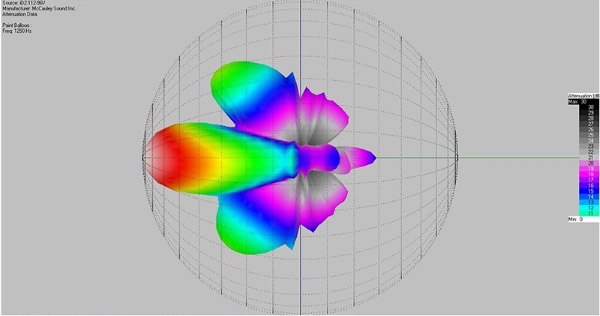
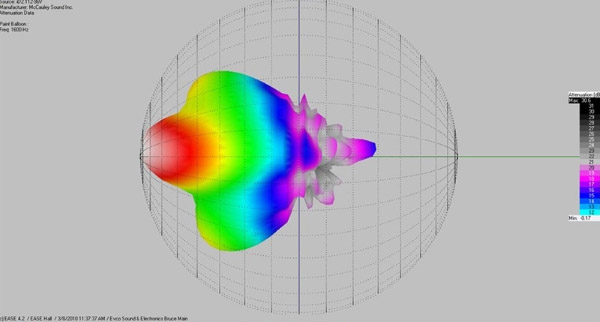
These lobes will vary in direction and intensity based on driver offset and pattern control, crossover slope, and overlap and alignment delay settings, but they will always occur in multiple driver boxes with physically separated sources. If a cabinet is laid on its side we get the same phenomena in the horizontal plane. Floor wedges, anyone?

This is one reason there has been resurgence in coaxial boxes. Because there is no vertical offset between the sources, we only have to correct for the variation in depth between the acoustic origin of the cone and the horn driver, and that distance stays more constant with off-axis listening positions.

The trade-off is that many coaxial designs use the driver cone as the horn flare to guide the high frequencies, and while this may be fine for monitors or other near-field applications, more precise pattern control is often required for sound reinforcement duties.

Baffles, Boundaries

The final piece of the directivity puzzle is the cabinet itself and the boundary effect created by setting it on something. Fractional space loading is created when we decrease the space that a device is radiating into.

As we saw in Figure 1, low frequencies are omnidirectional, so when we set a loudspeaker on the floor, we effectively halve its radiating space at low frequencies. This produces an additional 3 dB of output (double the power) in the hemisphere that it is still exciting.

If the baffle on the cabinet is physically large enough versus a given frequency, it can act as a boundary to create half space loading. This is what is sometimes called “baffle step.” In modern cabinets, the baffle is rarely much larger than the driver that is mounted in it, because generally, priority is given to things like weight, truck pack, handle location, flying hardware, arrayability and profile.

Technology has gone a long way towards providing a ton of output and fidelity from small packages. But physics hasn’t changed. When it comes to pattern control, size still matters!