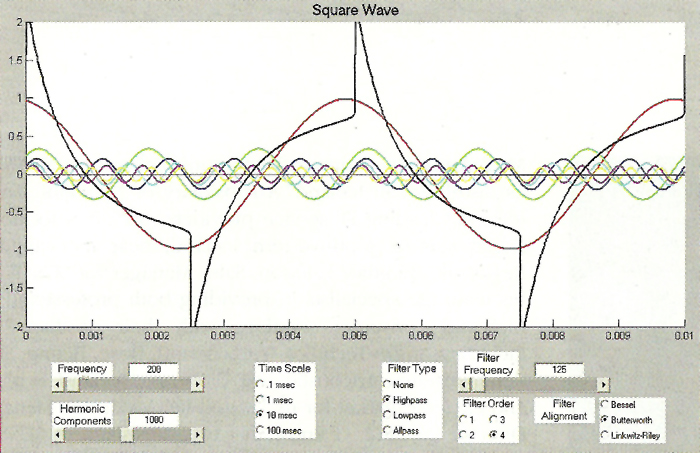
Hopefully you’ve noticed something interesting about the waveform after it was subjected to a high-pass filter (or an all-pass filter).
The phase shift of the components has caused the peak amplitude at the leading edge of the square wave to increase!
The amplitude of the raw square wave (no filtering) is approximately 0.79. After passing through the high-pass filter the peak amplitude is approximately 1.25.
Increasing the order of the filter or increasing the frequency (up to a limit related to the fundamental of the square wave) will increase the peak amplitude.
As seen in Figure 9, with a 4th order Butterworth high pass filter at 125 Hz the peak amplitude exceeds 2.2.
This is an increase of the peak amplitude of almost 280 percent compared to the amplitude of the original square wave!
This highly peaked waveform (no longer a square wave) results when the fundamental and some of the lower harmonics are shifted such that their positive peaks occur at, or very close to, the same time as the positive peaks of the other harmonics.
This also occurs for the negative peaks of the fundamental and the negative peaks of the harmonics. Careful inspection of Figure 9 will show this to be the case.
When signals are clipped by devices that do not have sufficient headroom to pass them the tops (and bottoms) of the waveform becomes flattened.
Whether the signal is periodic, symmetrical or asymmetrical, the flattening of a waveform (by design or by clipping) can only be accomplished via the addition of in-phase harmonics—just as in the case of a square wave.
If the clipping of the signal also results in the area bounded by the waveform above the time axis and below the time axis no longer being equal then a DC component has been introduced into the signal as well.
This, however, has no effect on the general shape of the waveform. If the DC component was somehow removed without otherwise affecting the signal, the waveform would simply experience a vertical shift, either up or down, depending on whether the DC component that was removed was greater than or less than zero.
I hope that this has helped to illustrate that it is the harmonic structure (content and phase relationship) of a signal that is responsible for flat-top shaped waveforms. Square waves are merely one example of these types of waveforms.