We’ve just discussed reflections based on the relative time arrival. Now let’s see how one dominant reflection can affect a frequency response based on its relative level.
A mathematical experiment is done using two Dirac/perfect impulses that are separated by 1 ms.
The delayed impulses (at 1 ms) are prepared at 0 dB, -10 dB, -20 dB and -40 dB relative to the 0 ms impulse and the frequency responses are observed.
This experiment will show the effect of a delayed signal, or in this case, assumed as reflection arriving at 1 ms relative to the direct sound at four different relative levels.
Side Note: A 3 dB difference in level is generally perceived as just noticeable and a 10 dB difference in level is generally perceived as twice/half of the loudness.
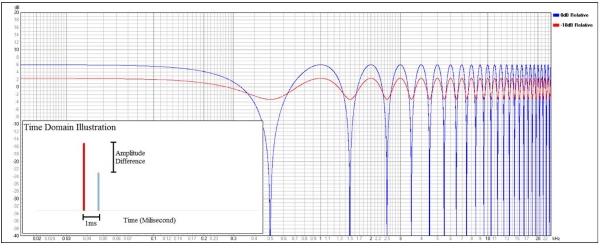
In Figure 6, the blue curve shows the resultant frequency response with 1ms delayed reflection with same amplitude with the direct sound.
The comb filtering contains deep notches and peaks.
1 ms is a period of 1000 Hz, calculated using the following equation:
Where T is period in second, and f is frequency in Hz.
A 1 ms reflection will create deep notches in frequency response at odd integer multiplies of half 1 ms wave period. Half 1 ms period represents a frequency of 500 Hz, thus notches can be observed at 500 Hz, 1500 Hz, 2500 Hz, etc.
A 6 dB peak/bump can be observed at integer multiplies of 1 ms wave period, which corresponds to 1000 Hz, 2000 Hz, 3000 Hz, etc. We can also observe that no summation/cancellation happens at frequencies 333 Hz, 666 Hz, 1333 Hz, 1666 Hz, etc. This is caused by 120-degree and 240-degree phase shift of the integer multiplies of 1 ms wave period.
At low frequencies, the frequency response is close to +6 dB. This happens because the phase shift is not significant for a larger wavelength (longer period of wave).
What happens if the reflection is -10 dB relative to the direct sound? Referring to Figure 6 again, the red curve shows the resultant frequency response. The notches and peaks are not as extreme as the blue curve. The comb filter shows peaks and dips at ±3 dB.
This variation in frequency response is not very audible and the delayed reflection is practically masked by the direct sound. In the recording world, a microphone placement technique called 3:1 ratio will result in -10 dB sound leakage. By doing this, the sound spill/leakage is practically masked by the main signal.
While 10 dB difference seems adequate for masking a signal in recording/listening purposes, the effect in frequency response (±3 dB) is still considered a lot.
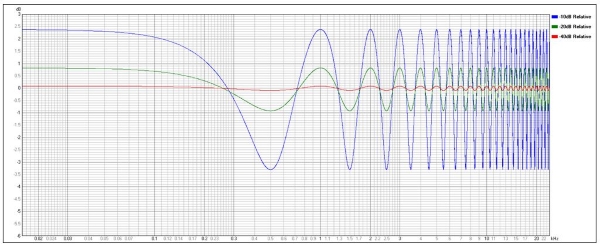
Figure 7 shows a frequency response comparison with delayed reflection at -20 dB (green curve) and -40 dB (red curve). It’s clear if one wants to minimize the effect of a reflection, a 20 dB or more attenuation is recommended.
Absorbers or diffusers can be used to attenuate specular reflections. By properly placing absorbers/diffusers, one can shape the room impulse response to specific acoustic needs, i.e., a recording studio, lecture hall, music hall, etc.
Side Note: Comb filter does not look good on the graph, but it does not always sound bad. For example, a concert hall generates comb filter due to the massive reflections, but it sounds good.
Small Room Acoustics
To listen to a sound source without any room effect, one must go outside although most likely listening outdoors is still going to be affected by a floor reflection. A room with a dimension less than 10 m/33 ft will give strong effects to a sound source. Reflections create acoustical distortions such as comb filter, room resonances, and boundary interference/loading.
Comb Filter
Nearby furniture and walls will give strong specular reflections. Unless absorbers or diffusers are installed at the point of reflection, these reflections may arrive with minimum attenuation and will result in a strong comb filter. This is easily noticed at high frequencies. Refer back to Figure 3, where the blue curve shows strong comb filtering at high frequencies (greater than 500 Hz).
A high-frequency comb filter is easily controlled by using absorbers, diffusers, or by slanting the wall. Aside from room modification, sound source’s types, placements and orientations also have a lot of effects.
Placing a loudspeaker too close to a boundary, such as on the table or too close to a reflective side wall, can result in a strong reflection that can’t be easily attenuated. Typical perception of comb filtering is a hollow or harsh sound reproduction at mid/high frequency.