In part 1 of this series (here), we introduced basic digital audio concepts, the FIR filter, and also compared IIR & FIR filters in terms of EQ performance and impulse response length. Now let’s continue the comparison, considering computational complexity and the key benefits of FIR filters.

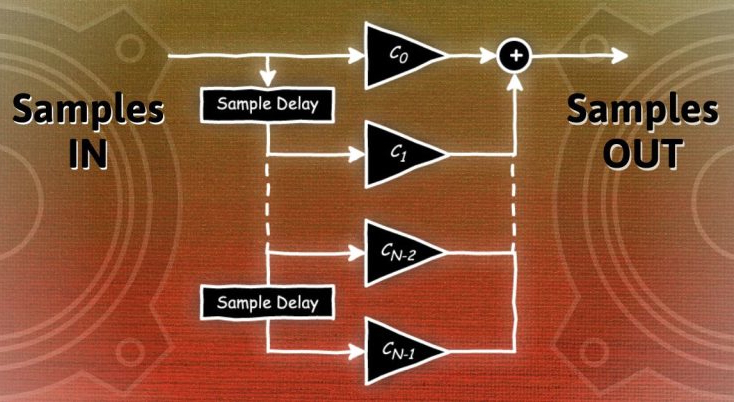
As previously noted, FIR filters are more computationally costly than IIR filters. Consider some of the simple IIR and FIR filters shown in Figure 1. When estimating and comparing computational costs, we generally look at the mathematical operations – multiplications and additions. We assume that a processor can calculate a “multiply” and an “add” effectively in the same operation; therefore, we can ignore the additions and just count and compare the multiplications.

The 1st order IIR filter has three coefficients that need to be multiplied with the audio samples, and so we estimate the filter to take approximately 3x the sample rate operations per second. The FIR filter has N coefficients (where N is the filter length) and so we estimate the FIR filter to take N x the sample rate operations per second. Table 1 compares the Figure 1 filters.

In part 1, we’ve seen in the examples how approximately 40 taps or more are needed for the FIR filters to approximate the IIR filters, and Table 1 shows that this comes at the computational cost of 8 times or 13.3 times that of the IIR.

Typical Processor Output Channel. As at the writing of this article, a common high-end speaker processor has approximately 24 IIR biquads for high-pass (HP), low-pass (LP), shelf and parametric filters, and 2048 taps of FIR. Table 2 compares the computational cost of both.

FIR Filter Benefits

If FIR filtering is so computationally costly, what are its advantages? There are two primary benefits:

1) Independent control of magnitude and phase, and

2) More detailed equalization (including easier filter creation from a desired frequency response).

Let’s explore each of these further.