The topic of architectural acoustics has been documented and carefully studied for more than a century. Historically, most acoustic treatment products and schemes have offered a relatively “broadband” approach in order to reduce reverberation time in a room. While these fundamentals have changed little, treatment materials and techniques have gradually advanced.
Parametric acoustics does not challenge the physics underlying traditional acoustic theory. Rather, it offers a fresh perspective on how the application of new materials can and should be employed.
This thesis expands my T60 Slope Ratio theory by providing methodology, commentary, and examples for specifying acoustic treatments as band-limited tools. The goal of this paper is to demonstrate how one can achieve “Good” to “Optimum” T60SR6 scores in any performance venue. The T60 Slope Ratio is represented symbolically as T60SR6. The calculation delivers a relational score – using the two extreme time values from the six octave centers – between 63 Hz and 2 kHz.
To that end, the next level of architectural acoustic refinement is proposed: PMAT – the Parametric Method of Acoustic Treatment. While the best practitioners in architectural acoustics already understand, and may implement similar principles, the PMAT concepts are not widely considered or applied.
Background
The idea of a generalized, single number reverberation time is merely a convenient way of stating a room’s averaged, mid-band (500 Hz and 1 kHz) reverberation time (T60). For most end users, acoustics boils down to this single number concept. It’s not uncommon to hear someone say, “I think we have too much reverb and we want something less, or shorter.”
Knowingly or not, they’re almost always referring to the mid-band average. Unfortunately, this commentary often leads to the ubiquitous, 1- or 2-inch, fabric-wrapped fiberglass panels or similar foam products.
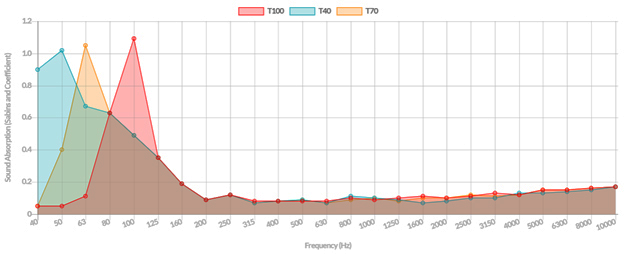
Notice the common theme with each of the products shown in Figure 1 above: very small absorption coefficient (α or alpha) values at 250 Hz and below, then a quick rise to much more useful numbers, starting at roughly 500 Hz. Fundamentally, these type materials are performing as 500 Hz, low-pass, reverberation filters.
As you continue to read through this article, notice that none of the room examples shown below match up very well with these popular treatment products.
Line Charts
Using line charts is probably the easiest way to visualize reverberation time at the various critical frequencies. They’re also a good way to graphically show alpha data. “A line chart is a type of chart which displays information as a series of data points called ‘markers’ connected by straight line segments.” [1]
For this thesis – unless otherwise noted – one-octave frequency centers are used, between 63 Hz and 4 kHz. Also, 1/3-octave bands can and should be used if a room exhibits an unusually high or a non-linear distribution of resonance or reverb between the octave centers.
Needs Analysis
Every room or building has some inherent acoustic “sound” or tonal character. A few are complementary to their various sound-related functions, others are obviously bad, even to the ear of the non-professional. The vast majority fall somewhere in between, and do not fully reveal their strengths or weaknesses until certain sonic activities are introduced.
The exceptional rooms generally go unnoticed to all but a few, whereas really bad rooms seem non-functional to almost everyone; usually because they have too much reverberation for almost any application. One example is a high school gym I reviewed many years ago. There was so much reverberation the coaches couldn’t hold basketball or volleyball practice. They couldn’t communicate with the players. The %ALcons score was 33, which translates to an STI score of 0.30; both are considered “bad” results.
Under these conditions, the obvious solution is lots of broadband absorption. Because this building wasn’t a performance venue, and didn’t require custom or specialized treatment, the solution was the application of about 9,000 square feet (ft2) of International Cellulose K13, sprayed onto the ceiling – to a thickness of 1.5 inches.
While this was an extreme example, most facilities have more specific needs. If we’re within one second or so of an appropriate mid-band reverberation time, it is suggested here that using only broadband absorption is not the optimal solution.
Most broadband treatment materials (like those shown in Figure 1) provide little absorption at or below 250 Hz. This is a problem because these days many performance, worship, and entertainment venues can’t dissipate the massive amounts low and very low frequency energy as quickly as it’s being produced. Even open-office environments can fall into this trap, as the lower frequencies of the human voice tend to travel through a room more easily than the mid- and high-frequencies.

To further complicate matters, it’s also likely that the 63 Hz and 125 Hz octaves aren’t the only ones with T60s that are too long, relative to their neighboring frequencies above. When these scenarios exist, the room’s reverberant character is even more out of balance and may need to be acoustically “equalized.”
About two years ago, I began disseminating the T60 Slope Ratio thesis, which outlines the optimal relationship of reverberation time, at the octave centers, between 63 Hz and 2 kHz. The Slope Ratio thesis prescribes a set of design and performance goals but doesn’t offer any specific treatment guidelines. PMAT builds on this new model of refinement in architectural acoustics.
PMAT Defined
The Parametric Method of Acoustic Treatment (PMAT) suggests that acousticians specify absorption materials that perform most of their work within various 1- to 2-octave bands. Think of these products as 1- to 2-octave, cut only, parametric absorbers (room-tone equalizers).
An audio parametric equalizer offers separate controls for frequency, bandwidth (Q), and level. When properly applied, these are powerful tools. If we adapt those same three parameters to a product’s alphas, we introduce a completely fresh, band-specific way of treating excess reverberation.
● Frequency: The center frequency of maximum absorption offered by the treatment material.
● Bandwidth: How broad or narrow is the Q? PMAT suggests that when the α rate is reduced by 25 percent or more – one octave above and below its peak α – and continues along at a similar trajectory, then the product may be well-suited for PMAT applications.
● Level: Higher alphas are better because the higher the α, the more efficient the product is at absorbing energy at that specific frequency. This translates to less material being needed per frequency band, and lower overall cost.
The T60 Slope Ratio thesis directs us to look at the six octave centers between 63 Hz and 2 kHz. And, while the most problematic frequency is often 63 Hz, it’s not always the longest T60.
In a well-behaved room, regardless of mid-band time, the slope of its T60 line chart will gradually decrease, beginning with the lowest frequency analyzed. When a room presents an “asymmetrical, or non-linear” Slope, any of the six octaves may contain longer or shorter reverb times than their neighbors. Ideally, those anomalies can and will be addressed using PMAT solutions.
Further, this article extends the scope of analysis up to 4 kHz, because most treatment datasheets commonly provide that frequency. However, dealing with excess 4 kHz reverberation is rarely an issue.
Absorption Coefficients Above 1.0
The sound absorption coefficient is the fraction of sound energy absorbed by a material. Expressed as a value between 1.0 = perfect absorption (no reflection) and 0 = zero absorption (total reflection). The value varies with frequency and angle of incidence, determined experimentally. [2]
If you’re disturbed by the various charts in this document showing alphas higher than 1.0, know that I’m aware of the arguments for and against. I’m using published data from the various manufacturers. If preferred, round down to 1.0. By lowering to a max α of 1.0, your results will merely reflect the need for slightly more material.
Current High Q Products
Wouldn’t it be great if there were lots of options for treatment based on selective, narrowband absorption? And, wouldn’t it be cool if those options included both velocity- and pressure-based absorption schemes? If you’re unfamiliar with the differences between velocity- and pressure-based absorption, a short article from GIK Acoustics (“Understanding Different Bass Trapping” at gikacoustics.com) is quite concise.
Finding existing products to fit the specific needs of a given project can be difficult. I’ve spent considerable time looking and will share several examples below. Hopefully, in the near future, more manufacturers will see the value in developing band-specific absorption products.
When considering bass frequency treatments, it’s important to determine how a manufacturer’s absorption data was measured in the 63 Hz and 125 Hz bands. Some companies provide their α data based on impedance tube measurements, which only give normal incidence alphas. A very large reverberation chamber is needed to accurately measure random incidence sound absorption coefficients.
Remember, it’s necessary to view these charts as inverted, parametric cut filters. The higher the peak α, the deep the acoustical cut.
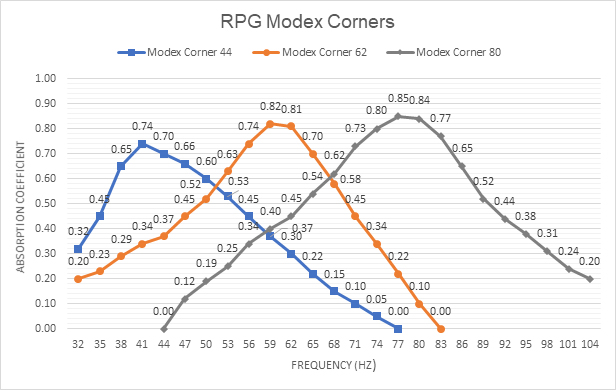
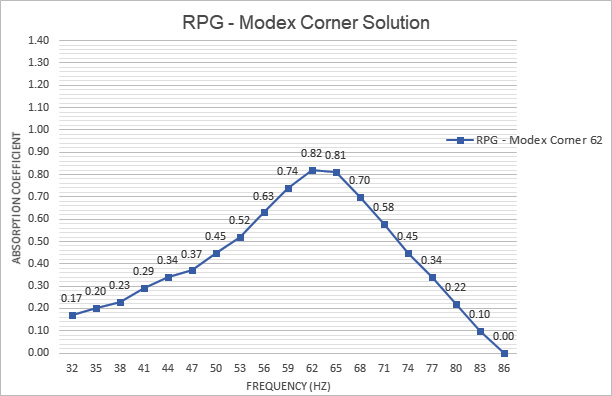
Both RPG and GIK Acoustics show dedicated “bass trap” products that appear to represent what we’re looking for at 100 Hz and below. For example: Look at the α chart for the GIK Scopus series, and the RPG Modex Corner series bass traps (Figures 2 and 3). These examples show significantly lower alphas above and below their peak absorption frequency.
Moving up to 125 Hz: The RPG Modex LF product has a very nice α chart that peaks at 125 Hz (Figure 4).
Next up, 250 Hz: The Kinetics Noise Control (KNC) Sereno 2/10 2-inch FG perforated wood panel (again, Figure 4) fits nicely into the PMAT scheme. Notice how quickly it falls to 0.38 at 125 Hz and 0.66 at 500 Hz. Also, you can see how this panel is used to address the 250 Hz slope asymmetry in Figures 6 and 7.
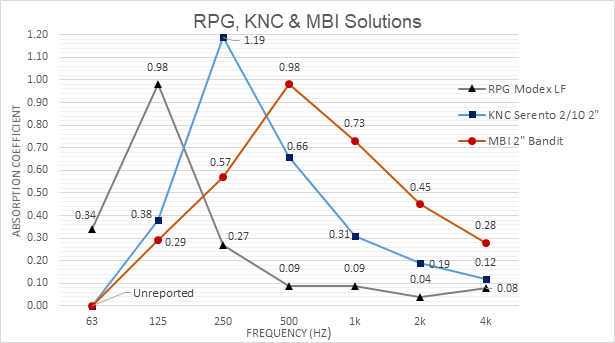
Figure 4 also shows the best 500 Hz example I’ve found: the MBI 2” Bandit series. It has a slightly broader Q at 1 kHz, but overall it fits well into the portfolio.
1 kHz: The 1.2-inch RPG BAD Panel (Figure 5) actually peaks slightly lower at 800 Hz, but it’s the closest option I’ve found for addressing 1 kHz. It’s really best applied when a little broader PMAT solution is needed. I have yet to find anything that specifically addresses 2 kHz and above, but those frequencies are rarely a major concern.
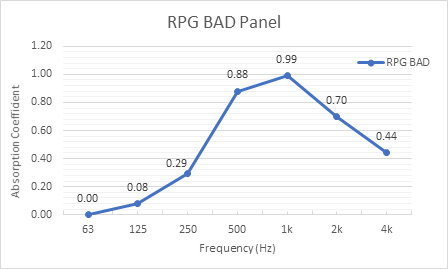
By now you should see how the PMAT theory is applied. As always, the application of these treatments needs to be well distributed and properly placed to maximize their effectiveness.
Warnings For Absorption Coefficient Specs
The α values of any treatment solution should have a certified laboratory report that can be easily accessed from the manufacturer’s website. The basic assumption is the data follows standardized ISO or ASTM testing procedures.
One caution: When evaluating treatment materials, check whether metric or imperial Sabins are being stated. The Sabin is the unit of measurement used to describe a unit of sound absorption. “One square meter of 100 percent sound absorbing material has a value of 1 metric Sabin. One square foot of 100 percent sound absorbing material has a value of 1 imperial Sabin.” [2]
Also, beware that some manufacturers state the absorption data per square foot (or meter) of exposed surface material on some items, but for other products they report the data for the unit as a whole. If the data is clearly marked as representing a “per panel” value, it’s fairly easy to calculate back to a value that represents the α per square foot or meter.
One way to spot the difference is to watch for alphas that are way above 1.0, and often above 2.0. If you see this, there’s a good chance the data is being expressed for a whole panel. Example: A 2- by 4-foot panel has 8 ft2 of surface on one side. Divide the per-panel Sabins total by 8 to get the α per square foot.
Adding Sabins From Different Materials
How do the various α values add together, at any given frequency, when working with treatments having disparate alphas? The answer is to convert the various alphas into total Sabins of absorption at each frequency of concern.
Let’s say you have 128 ft2 of a treatment that has an absorption coefficient of 0.60 at 500 Hz, and 128 ft2 of another product that has an α of 0.35 at the same frequency. You don’t get to add the alphas together. Based on area, you have to calculate the total Sabins of each, then add those numbers together.
Example: 1280.60 = 76.8 Sabins of absorption from material A, and 1280.35 = 44.8 Sabins from material B. Together, these add up to a total of 121.6 Sabins of absorption at 500 Hz.
To help organize and crunch these numbers I built a Rough Order of Magnitude (ROM) Sabins calculator (Figure 6) This is a statistical calculator that requires T60 data from an existing room if you want to calculate before and after treatment results. For budgetary planning, it’s a reasonably objective way to estimate the type and approximate square footage needed to reach new T60 goals.
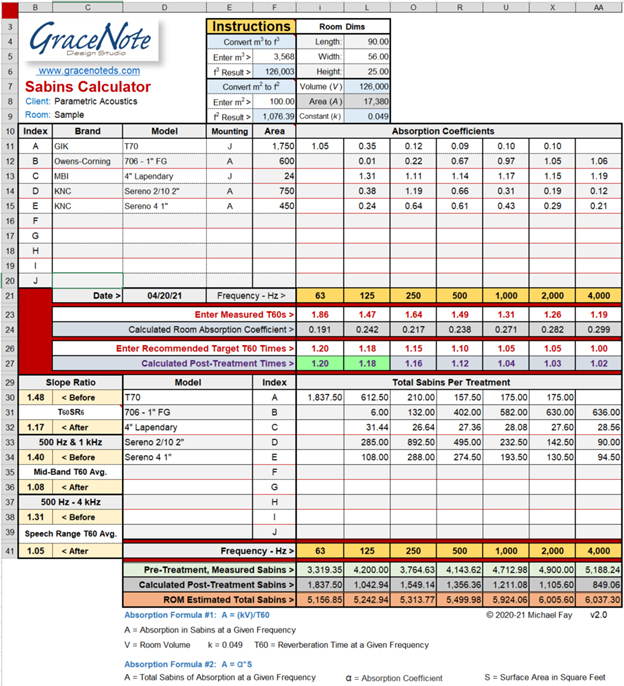
For rows 11-20, Column F is used to input and manipulate the total area needed for the proposed treatment materials. The before and after results can be seen graphically in Figure 7. (The spreadsheet calculator can be downloaded from the GraceNote Design Studio, gracenoteds.com/more.)
The measured T60 data establishes the existing conditions in a room. The existing conditions are described as “Room Absorption” (RA), which is the sum of Sabin absorption due to objects and surfaces in a room, and due to dissipation of sound energy in the medium (air) within the room.” [2]
To calculate the existing RA for each frequency, the measured T60 times are input along row 23. The absorption coefficients will be automatically calculated along row 24, using Sabine’s classical formula.
Row 26 is where desired or target T60 times are input. The underlying formulas in Row 27 calculate the effects of the various treatment alphas, based on the total square footage of each material applied at each frequency. The cells in row 27 turn green when you’ve found an exact match.
It’s not necessary to perfectly match the times in rows 26 and 27, but the row 27 values should come close. Try to stay within +/- 0.10 of a second. Note that 4 kHz may be the hardest to match but it’s the most forgiving, so +/- 0.15 seconds or so should be close enough.
One more caveat: As stated earlier, this is a ROM estimator. It’s impossible to calculate and predict perfect results. This calculator is simply a tool to help organize the data and streamline the numerous calculations that would otherwise be tedious to process.
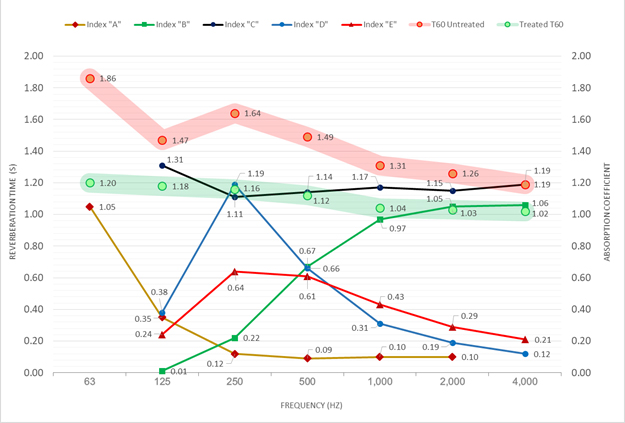
The Figure 7 line chart displays all the key numbers shown in Figure 6. It shows the non-linear T60s of a hypothetical, untreated room, the room’s proposed target values, and the absorption coefficients for each of the materials selected to reach the various goals. The slope is considered non-linear because the decay times do not gradually decrease as the frequencies get higher.
More Examples With Varying T60 Profiles
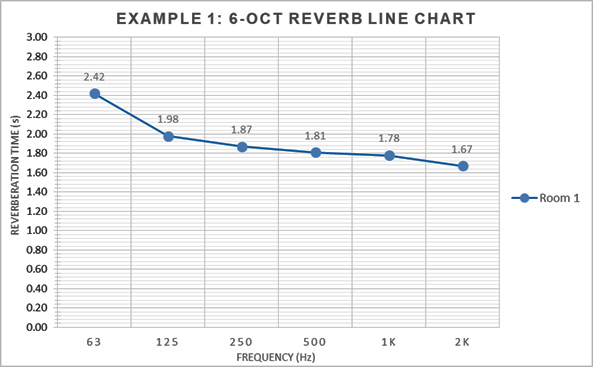
Here are two additional examples of how PMAT solutions might be applied. The first room is highly reverberant, with a mid-band T60 of 1.80 seconds. It also rises to 2.42 seconds at 63 Hz. It isn’t too difficult to reduce the overall mid- and high-frequency T60s, but to bring the Slope Ratio into at least a “Good” grade, the 63 Hz octave must be addressed. Untreated, this example gets a “Fair” grade based on a T60SR6 score of 1.45.
Example 1: Currently, I know of no single product that can fully address every T60 adjustment that may be desired. At least two PMAT filters need to be applied, maybe more. Notice the similarity between the shape of the T60 line charts and the alphas of the potential treatment solutions. This is what we’re looking for from all parametric treatment products; the longer the T60 at any given octave center, the greater the absorption coefficient we want at that same octave center.
Figure 8 depicts a classic, and far too common, environment. Generally, this room may be appropriate for mass choir, pipe organ and/or orchestra. Unfortunately, it’s not acoustically “friendly” for modern-day amplified music, nor the spoken word.
In this example, the client and acoustic consultant need to thoroughly discuss the desired T60s and Slope Ratio scores with all new or predominant audio applications in mind. For venues used for 21st century amplified music and production, the acoustician’s specifications should optimize an appropriate mid-band T60, while simultaneously applying customized PMAT solutions to achieve the best possible Slope Ratio score.
Figure 9 shows one way this might be accomplished. Of course, the exact quantity and location of each treatment material requires some careful analysis, but the basic tools are there to address the needs of this room with PMAT techniques.
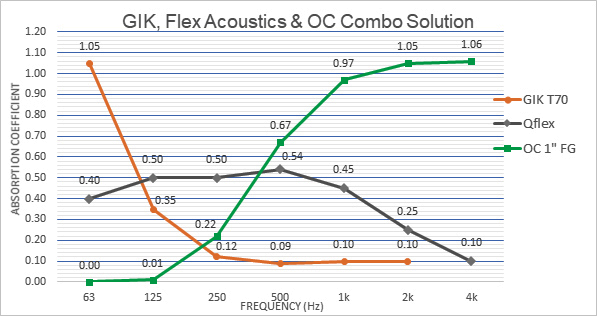
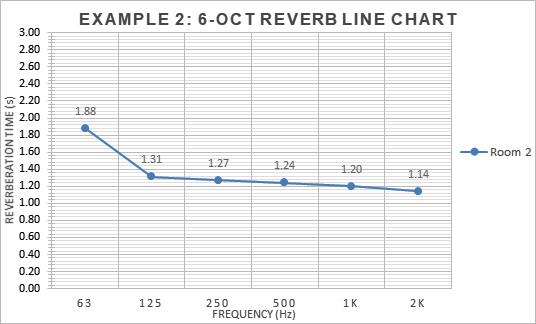
Example 2: This room (Figures 10 and 11) exhibits a reasonable mid-band T60 for amplified music and spoken word, but 63 Hz is problematic. The mid-band T60 is 1.22 seconds, but the Slope Ratio score is 1.65. Subjectively, this is considered a “Poor” grade.
For a room like this, the primary goal is to reduce the 63 Hz T60 without absorbing too much reverb at any higher frequency. In order to accomplish this, a product such as shown in Figure 11 might be an appropriate option.
Example 3: Figure 12 depicts not a single room, but an aggregate of the ten best and worst venues for amplified music in Denmark [3]. It should be obvious that even the best rooms won’t sound good and “tight” in the spectrum serviced by subwoofers.
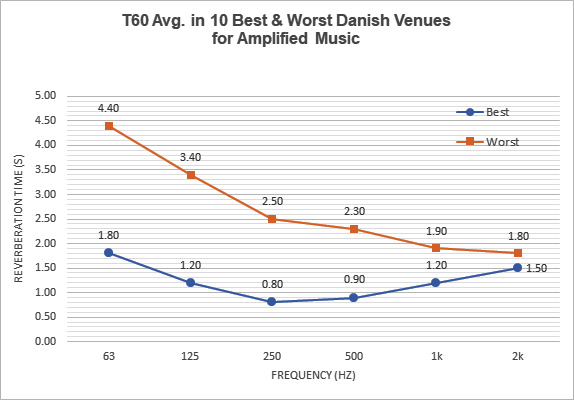
These line charts show how widely the reverberation time can vary from room to room. And, even the average labeled “best”, represents a T60SR6 score of 2.25, which is considered “Bad.” While this is a relatively small sample size, the trend is obvious: none of these rooms was designed with our modern musical tastes and technologies in mind.
Final Thoughts
When I began my career in pro audio and acoustics, I never expected to find myself so focused on reverberation. Over the years, one of my prime tenets has been to look for the weakest link in my professional toolbox, then work to strengthen it as much as possible.
The more I’ve studied and applied various acoustic principles, the more I believe the weak link in architectural acoustics is the nearly-complete lack of interest by most to identify and treat resonant and reverberant energy – at and below 125 Hz.
Some may argue that applying the PMAT approach is too much trouble, or too expensive. The same was probably said about Dr. Peter D’Antonio’s QRD diffusor systems back in the early 1980s. But today, diffusors of various types and sizes are commonly specified and installed.
For those who wish to optimize all possible acoustic aspects of their built environments, I believe the results achieved when applying the Parametric Method of Acoustic Treatment will justify any moderate, additional investment.
Change will no doubt come slowly; it may take years to see common usage of the PMAT techniques. My hope, however, is to spark industry awareness and launch this topic into the mainstream of architectural acoustic solutions.
References
[1] https://en.wikipedia.org/wiki/Line_chart
[2] http://www.acoustic-glossary.co.uk/
[3] https://flexac.com/en/about/brochure/ (see aQtube-aQflex pdf)
The author offers his special thanks to the following people on a peer review panel for the comments and corrections they provided during the development of this thesis: Neil Thompson Shade, FASA – Acoustical Design Collaborative; Hadi Sumoro, HX Audio Lab; and Steven Liddle, Springwell Audio AB.